Beispiel, dass auf eine quadratische Gleichung führt

1.Gegeben:
Als nächstes betrachten wird die Gleichung mit einer Potenz:

2.Substitutionsgleichung aufstellen:

Hier kommt zweimal der gleiche Logarithmus log10(x–90) vor. Wir ersetzen
(substituieren) den Logarithmus durch u, d.h. die Substitutionsgleichung lautet:

3.Substitution:

Wir ersetzen den Logarithmus durch u:

Wir bringen die alle Summanden auf die linke Seite:

Dies ist eine quadratische Gleichung, die wir mit der Lösungsformel lösen.
Die Lösungsformel für quadratische Gleichungen lautet:

Wir setzen die Koeffizienten der quadratischen Gleichung in die Lösungsformel ein:

Wir vereinfachen und erhalten:

Wir vereinfachen nochmal und erhalten:

4.Rücksubstitution:

Nun wollen wir die Rücksubstitution durchführen, d.h. wir setzen das Ergebnis u=1
in die Substitutionsgleichung (2) ein:

Um diese einfache Logarithmusgleichung zu lösen, benutzen wir
wie üblich die Definition des Logarithmus" aus Kapitel 1:

Umstellen nach x ergibt das Ergebnis:

  

5.Die Probe:

Eigentlich wäre hier keine Probe nötig. Wir hatten aber vereinbart,
daß wir die Probe prinzipiell immer durchführen wollen:

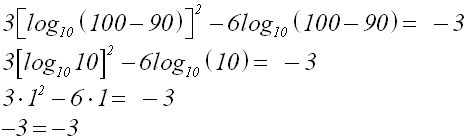
Es ergibt sich eine wahre Aussage. Die Lösungsmenge lautet also:

6.Lösungsmenge: