Logarithmusgleichung mit Logarithmus im Exponenten Als nächstes betrachten wir Logarithmusgleichungen, bei denen der Logarithmus im Exponenten einer Potenz steht. Der Definitiosbereich ist D={x|x>0}, denn ein Logaritmus ist nur für positve Zahlen definiert. Den ersten Summanden können wir mit Hilfe eines der Potenzgesetze als Doppelpotenz schreiben: 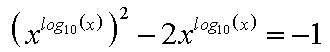Substitution: Jetzt können wir die Substitution durchführen: 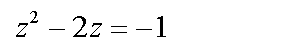Wir bringen die Zahl (–1) auf die andere Seite, indem wir auf beiden Seiten 1 addieren. Wir erhalten eine quadratische Gleichung: 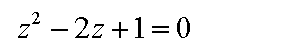Die quadratische Gleichung lösen wir mit der allgemeinen Lösungsformel. Sie lautet: 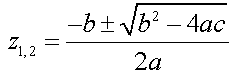Wir setzen die Koeeffizienten der quadratischen Gleichung in die Lösungsformel ein: 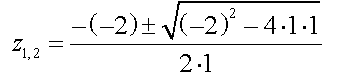Wir vereinfachen und erhalten das Ergebnis z=1: 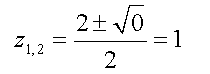Rücksubstitution: Nun führen wir die Rücksubstitution durch: Dann logarithmieren wir beide Seiten: 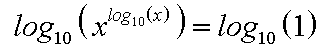Jetzt wenden wir das 3.Logarithmusgesetz an. Übrigens dürfen wir es anwenden, weil x positiv ist, denn sonst wäre log10(x) nicht definiert. 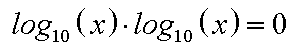Jetzt benutzen wir den bekannten Satz: Ein Produkt ist gleich Null, wenn eines der Faktoren gleich Null ist (alternativ könnte man auch auf beiden Seiten die Wurzel ziehen) Wir wenden die "Defintion des Logarithmus an", und erhalten das Ergebnis: Probe: Die gegebene Gleichung lautete: Wir setzten das Ergebnis x=1 in diese Gleichung ein: log10(x) ist gleich 0. Daher vereinfacht sich die Gleichung zu: 2·0=0, und daher: Die ursprüngliche Gleichung hat den Definitionsbereich D={x|x>0}. Für alle x>0 gilt aber: x0=1 Wir erhalten eine wahre Aussage. Daher ist x=1 eine tatsächlich eine Lösung Lösungsmenge: