|
In diesem Abschnitt werden wir
zeigen, wie man manchmal eine Logarithmusgleichung lösen
kann,
deren Logarithmen verschiedene Basen haben.
Gegeben sei das Beispiel:
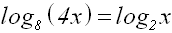
Wir benutzen den Basiswechselsatz, um die Basis
des Logarithmus
auf linken Seite umzuwandeln. Der
Basiswechselsatz lautet:
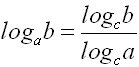
Somit ergibt sich:
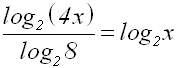
Den Nenner kann man vereinfachen, denn log28=3
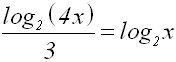
Die "3" im Nenner bringen wir auf die andere
Seite, indem
wir beide Seiten der Gleichung mit 3
multiplizieren:
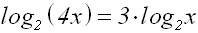
Den Faktor "3" vor dem Logarithmus beseitigen
wir,
indem wir die 3.Logarithmusformel anwenden:
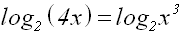
Wie im Kapitel 3 erklärt, dürfen wir die Numeri
gleichsetzen:
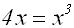
Wir bringen alle Summanden auf eine Seite, indem
wir 4x auf beiden Seiten subtrahieren:
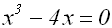
Wir klammern x aus:
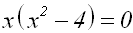
Die Lösungen der Gleichung sind:
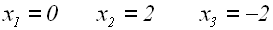
Die Probe ergibt, daß nur x=2 eine Lösung ist,
denn
ein Logarithmus ist ja nur für positive Numeri
definiert:
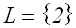 |