 |
Potenzrechnung: Der Potenzwert ist
gesucht |
|
Im Kurs Potenzrechnung haben wir uns
mit Potenzen beschäftigt:

Dabei war der Potenzwert gesucht. Im folgenden bezeichnen wir
die gesuchte Größe jeweils mit x:
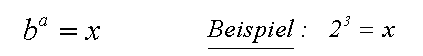 |
 |
Wurzelrechnung: Die Basis ist
gesucht |
|
Im Kurs Wurzelrechnung haben wir uns
dann mit dem Fall beschäftigt,
daß die Basis einer Potenz gesucht war, die wir a-te Wurzel aus c nannten:
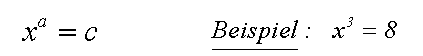
Im allgemeinen will man eine Lösung nach der Unbekannten x umstellen
können. Um diese Gleichung nach der Unbekannten Wurzel x umstellen
zu können, hatten wir das Wurzelzeichen eingeführt:

|
 |
Logarithmenrechnung: Der Exponent
ist gesucht |
|
Natürlich gibt es eine dritte
Möglichkeit: Statt dem Potenzwert c oder
der Basis b kann auch der Exponent gesucht sein (den wir wieder x nennen):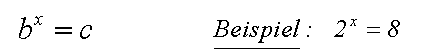
Man nennt den (unbekannten) Exponenten dann den Logarithmus
von c zur Basis b (im Beispiel den Logarithmus von 8 zur Basis 2).
Um die Gleichung bx=c nach der Unbekannten x (dem Logarithmus)
umstellen zu können, müssen wir auch hier ein neues Zeichen einführen.
Als Zeichen für den Logarithmus schreibt man "log":
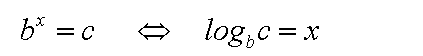
Wir sprechen: Logarithmus von c zur Basis b.
Im Beispiel: Logarithmus von 8 zur Basis 2
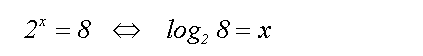
Zusammenfassung:
Unter dem
Logarithmus x=logbc versteht man
den Exponenten x in der Gleichung bx=c
(gesprochen: Logarithmus von c zur Basis b) |
|