| Definition |
 |
Definition |
|

|
 |
Notwendig der Einschränkungen
b>0, b 1 1 |
|
Wir wollen nun erklären, warum die
Forderung b>0 bei der
Definition notwendig ist.
Zunächst erklären wir warum b=0 verboten ist.
Dazu formen wir die Logarithmusform in die Potenzform um:

Die Gleichung 0x=10 ist unlösbar, denn
Null hoch irgendeine Zahl x
ist immer gleich Null. Deshalb dürfen wir die Zahl Null als
Logarithmusbasis nicht zulassen.
Das gleiche passiert, wenn wir eine negative
Logarithmusbasis zulassen:

Auch diese Gleichung ist unlösbar.
Als dritten Fall müssen wir noch die Basis b=1
ausschließen. Den Grund
sehen wir wieder, indem wir die Logarithmusform in die Potenzform umformen:
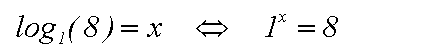
Egal welche Zahl wir für x einsetzen, der Potenzwert kann nie 8 werden,
denn 1 hoch irgendeine Zahl ergibt immer 1, aber niemals die Zahl 8.
|
 |
Notwendig der Einschränkung:
c>0 |
|
Nun wollen wir erklären, warum die
Forderung c>0 in der Definition notwendig ist.
Zunächst erklären wir warum c<0.
Dazu formen wir wieder die Logarithmusform in die Potenzform um:
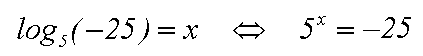
Die Gleichung 5x=–25 ist unlösbar,
denn wenn man eine positive Zahl
potenziert kommt auch immer eine positive Zahl heraus.
Und weil eine positive Zahl beim potenzieren eine
positive Zahl ergibt,
müssen wir auch die Zahl Null als Numerus ausschließen:
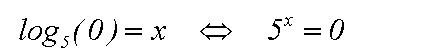
Weil zur Lösung der letzen Gleichung häufig Fragen auftreten sei angemerkt:
x=0 ist keine Lösung der Gleichung 5x=0, denn 50=1 (siehe Potenzrechnung).
|
|