Version: 2.00 ©Raddy '99	Inhalt zu: Binäre Logik II zurück
Info-Seite	Vorkenntnisse: ... Themen: ... Infos: www.mathematik.net
Unabhängige Aussagen	Bei zwei unabhängigen Aussagen hat der Wahrheitsgehalt der einen Aussage keinen Einfluß auf den Wahrheitsgehalt der anderen Aussage: Beispiel: A: Ich habe ein Auto B: Morgen ist Vollmond
Die Äquivalenz Seite 1 von 3	Zwei Aussagen sind äquivalent, wenn sie nur in folgenden zwei Kombinationen auftreten: Beide wahr Beide falsch Beispiel: A: Heute ist Montag B: Morgen ist Dienstag Man schreibt: AB Man spricht dies: "A äquivalent B".
Die Äquivalenz Seite 2 von 3	Die möglichen Wahrheitswert-Kombinationen einer Äquivalenz kann man in einem Pfeildiagramm darstellen: 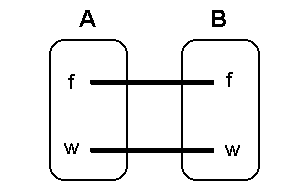Am Pfeildiagramm erkennt man die 4 Eigenschaften einer Äquivalenz: 1. Wenn A wahr folgt B wahr. 2. Wenn B wahr folgt A wahr. 3. Wenn A falsch folgt B falsch. 4. Wenn B falsch folgt A falsch.
Die Äquivalenz Seite 3 von 3	Man kann beweisen, daß aus den Eigenschaften 1 und 2 auch die Eigenschaften 3 und 4 folgen.
Die Implikation Seite 1 von 3	Zwei Aussagen A und B bilden eine Implikation, wenn sie in folgenden Kombinationen auftreten: Beide falsch Nur B wahr Beide wahr Beispiel: A: Ich habe einen VW-Golf B: Ich habe ein Auto Man schreibt: AB. Man spricht dies: "A impliziert B".
Die Implikation Seite 2 von 3	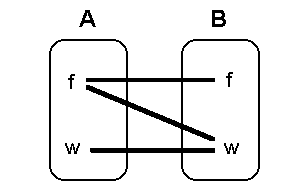Am Pfeildiagramm erkennt man die 2 Eigenschaften der Implikation: 1. Wenn A wahr folgt B wahr. 2. Wenn B falsch folgt A falsch. Wegen Eigenschaft 1 sagt man auch "Aus A folgt B" statt "A impliziert B".
Die Implikation Seite 3 von 3	Man kann beweisen, daß bei einer Implikation aus der Eigenschaft 1 auch atuomatisch die Eigenschaft 2 folgt.
Die Negation	Zu jeder Aussage A gibt es die zugehörige Negation A: A: Das Haus ist gelb A: Das Haus ist nicht gelb Eine Aussage A und ihre Negation haben immer einen entgegengesetzten Wahrheitsgehalt.