Version: 2.00
©Raddy '99

Binäre Logik II                  zurück
Unabhängige
Aussagen		 a-absatz.pcx (280 Byte)Beispiel
      Bis jetzt haben wir nur einzelne Aussagen betrachtet. In diesem
      Kapitel (Logik II) wollen wir zwei Aussagen betrachten, und ihre
      möglichen Beziehungen klären, in der diese Aussagen stehen können.
     
      Zunächst wollen wir den uninteressanten Fall betrachten, daß
      zwei Aussagen voneinander völlig unabhängig sind. Beispiel:

           Aussage A: Ich habe ein Auto.
           Aussage B: Morgen ist Vollmond.

      Nehmen wir z.B. an, die Aussage A sei falsch. Dann hat das auf
      die Aussage B (auf den Wahrheitsgehalt von B) keinen Einfluß.

      Genauso könnte man annehmen die Aussage A sei wahr. Auch dies
      hat auf den Wahrheitsgehalt der Aussage B keinen Einfluß. Die
      beiden Aussagen sind also vollkommen unabhängig.

a-absatz.pcx (280 Byte)Die Wahrheitswerte unabängiger Aussagen
       Liegen wie hier zwei vollkommen unabhängige Aussagen A und B vor,
       so können ihre Wahrheitswerte in vier Kombinationen auftreten, also
       in allen Kombinationen die möglich sind:

            1. A und B sind beide falsch:  Ich habe kein Auto und morgen ist kein Vollmond.
            2. A ist falsch und B ist wahr: Ich habe kein Auto und morgen ist Vollmond.
            3. A ist wahr und B ist falsch: Ich habe ein Auto und morgen ist kein Vollmond.
            4. A und B sind beide richtig: ich habe ein Auto und morgen ist Vollmond.

       Man bildet sozusagen das Kreuzprodukt der Wahrheitswerte von
       Aussage A mit den Wahrheitswerte der Aussage B.
       Dies kann man als Pfeildiagramm oder einer Tabelle darstellen: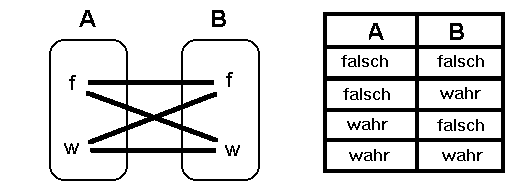

    11k2s2p1.pcx (4008 Byte)