Äquivalenz
Seite 3 von 3 |
 Vorbemerkung Vorbemerkung
Jetzt wird bewiesen, daß aus den Eigenschaften 1 und 2 sich die Eigen-
schaften 3 und 4 automatisch ergeben. Die vier
Eigenschaften lauteten:
1. Wenn A wahr
ist, folgt daraus, daß B wahr ist.
2. Wenn B
wahr ist, folgt daraus, daß A wahr ist.
3. Wenn A
falsch ist, folgt daraus, daß B falsch ist.
4. Wenn B
falsch ist, folgt daraus, daß A falsch ist.
 Beweis Beweis
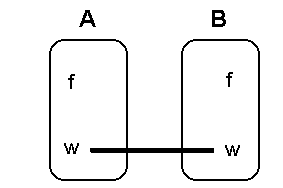 Aus den Eigenschaften
1 und 2 folgt Aus den Eigenschaften
1 und 2 folgt
der untere Strich im Diagramm.
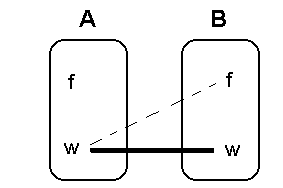 Wegen Eigenschaft 1
kann es aber Wegen Eigenschaft 1
kann es aber
keinen Strich von A(wahr) nach
B(falsch) geben (gestrichelte Linie).
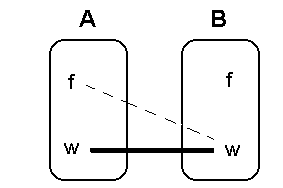 Ebenso kann es wegen
Eigenschaft 2 Ebenso kann es wegen
Eigenschaft 2
keinen Strich von B(wahr) nach
A(falsch) geben (gestrichelte Linie).
Somit treten also keine diagonal
verlaufenden Striche auf
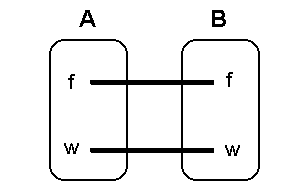
Nun bleibt nur noch zu beweisen, daß
es einen Strich von A=falsch nach
B=falsch gibt: Das Wort "wenn" in
Eigenschaft Nr.1 sagt, daß es auch ein
"wenn nicht" geben muß, d.h. den Fall
A=falsch. Aus A=falsch kann aber
nicht B=wahr folgen (wegen Eigen- schaft2), also gilt der obere Strich.
Das entstandene Diagramm gibt aber
nun alle 4 oben genannten
Eigenschaften wieder. Man kann also den Ausdruck A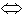 B lesen als: B lesen als:
"Aus A folgt B und aus B folgt A", ohne Eigenschaft 3 und 4 zu erwähnen.
|
 Aus den Eigenschaften
1 und 2 folgt
Aus den Eigenschaften
1 und 2 folgt Wegen Eigenschaft 1
kann es aber
Wegen Eigenschaft 1
kann es aber  Ebenso kann es wegen
Eigenschaft 2
Ebenso kann es wegen
Eigenschaft 2