Negation

Einführung am Beispiel:
      Im Kapitel "Binäre Logik I" haben wir erklärt, was eine Aussage ist.
      Zu jeder Aussage A gibt es die dazugehörige Negation dieser Aussage,
      die man mit ¬A bezeichnet. Beispiel:

         Die Aussage A hieße:                     Das Haus ist gelb.
         Die Negation von A heißt dann:     Das Haus ist nicht gelb. 

Wahrheitstabelle der Negation:
      Man kann die Wahrheitswerte, in denen die Aussagen A und ¬A
      auftreten, in ein Pfeildiagramm oder eine sogenannte 
      Wahrheitstabelle eintragen:
      
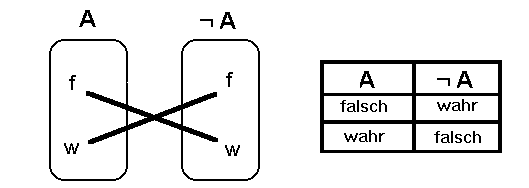      Achtung: Nicht jedes Pfeildiagramm, was so aussieht, stellt eine
      Negation dar, aber jede Negation hat solch ein Pfeildiagramm.

Eigenschaften der Negation
      Am Pfeildiagramm erkennt man zwei wichtige Eigenschaften:

         1. Wenn die Aussage A "wahr" ist, so ist die Negation ¬A "falsch".
         2. Wenn die Aussage A "falsch", so ist die Negation ¬A"wahr".

      Wir überprüfen Eigenschaft 1 und 2 am Beispiel:

            A:  Das Haus ist gelb.
          ¬A:  Das Haus ist nicht gelb

        zu 1. Wenn die Aussage "Das Haus ist gelb" wahr ist, 
                 ist die Aussage "Das Haus ist nicht gelb" falsch.
        zu 2. Wenn die Aussage "Das Haus ist gelb" falsch ist, 
                 ist die Aussage "Das Haus ist nicht gelb" wahr.