UND-Funktion
Seite 2 von 3
|
 W-Funktionen
Nun kann nicht nur eine Variable (Monatslohn) von zwei anderen
Variablen abhängig sein, sondern auch eine Aussage kann von
zwei anderen Aussagen abhängig sein. Ein Beispiel:
A: Mein Vater lebt noch.
B: Meine Mutter lebt noch.
C: Meine Eltern leben noch.
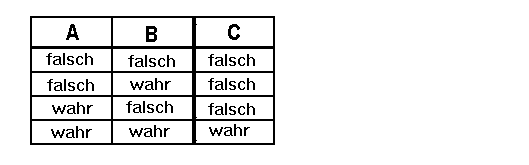
Man sieht: Aussage C ist nur wahr, wenn sowohl Aussage A
als auch Aussage B wahr ist. Aussage C ist also sowohl von
Aussage A als auch von Aussage B abhängig. Dies kann man
in einer Tabelle (Wahrheitstabelle genannt) darstellen: W-Funktionen
Nun kann nicht nur eine Variable (Monatslohn) von zwei anderen
Variablen abhängig sein, sondern auch eine Aussage kann von
zwei anderen Aussagen abhängig sein. Ein Beispiel:
A: Mein Vater lebt noch.
B: Meine Mutter lebt noch.
C: Meine Eltern leben noch.
Man sieht: Aussage C ist nur wahr, wenn sowohl Aussage A
als auch Aussage B wahr ist. Aussage C ist also sowohl von
Aussage A als auch von Aussage B abhängig. Dies kann man
in einer Tabelle (Wahrheitstabelle genannt) darstellen:
 Weil die Aussage C (d.h. ihr Wahrheitsgehalt) von den
Aussagen A und B abhängig ist, bilden die drei Aussagen eine
"Funktion zweier unabhängiger Aussagen", wobei A und B
die unabhängigen Aussagen sind, und C die abhängige Aussage.
Weil die Funktionswerte der Funktion keine Zahlen sind sondern
Wahrheitswerte (wahr oder falsch), gibt man solchen Funktionen
einen besonderen Namen: Wahrheitsfunktionen oder W-Funktionen.
Eine Wahrheitsfunktion kann man genauso in einem räumlichen
Koordinatensystem darstellen, wie eine "normale" Funktion
zweier unabhängiger Variablen doch dies ist nicht üblich.
Stattdessen wollen wir noch eine andere Darstellungsform
für eine W-Funktion kennenlernen:
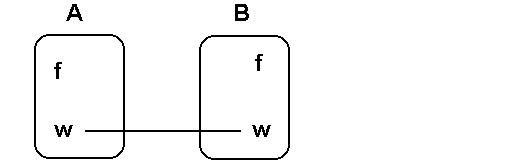
Man kann eine W-Funktion in einem Pfeildiagramm darstellen.
Dazu vereinbart man: Ist ein Wahrheitswerte von A mit einem
Wahrheitswert von B durch einen Pfeil verbunden, so hat die
Aussage C dort den Wahrheitswert (Funktionswert) "wahr",
ansonsten hat sie den Wahrheitswert "falsch":
Weil die Aussage C (d.h. ihr Wahrheitsgehalt) von den
Aussagen A und B abhängig ist, bilden die drei Aussagen eine
"Funktion zweier unabhängiger Aussagen", wobei A und B
die unabhängigen Aussagen sind, und C die abhängige Aussage.
Weil die Funktionswerte der Funktion keine Zahlen sind sondern
Wahrheitswerte (wahr oder falsch), gibt man solchen Funktionen
einen besonderen Namen: Wahrheitsfunktionen oder W-Funktionen.
Eine Wahrheitsfunktion kann man genauso in einem räumlichen
Koordinatensystem darstellen, wie eine "normale" Funktion
zweier unabhängiger Variablen doch dies ist nicht üblich.
Stattdessen wollen wir noch eine andere Darstellungsform
für eine W-Funktion kennenlernen:
Man kann eine W-Funktion in einem Pfeildiagramm darstellen.
Dazu vereinbart man: Ist ein Wahrheitswerte von A mit einem
Wahrheitswert von B durch einen Pfeil verbunden, so hat die
Aussage C dort den Wahrheitswert (Funktionswert) "wahr",
ansonsten hat sie den Wahrheitswert "falsch":
|