UND-Funktion
Seite 3 von 3
|
 Die UND-Funktion
Als wir auf der vorigen Seite erklärten, was eine W-Funktion ist,
taten wir dies an einem Beispiel:
A: Mein Vater lebt noch.
B: Meine Mutter lebt noch.
C: Meine Eltern leben noch.
Die dazugehörige Wahrheitstabelle lautete: Die UND-Funktion
Als wir auf der vorigen Seite erklärten, was eine W-Funktion ist,
taten wir dies an einem Beispiel:
A: Mein Vater lebt noch.
B: Meine Mutter lebt noch.
C: Meine Eltern leben noch.
Die dazugehörige Wahrheitstabelle lautete:
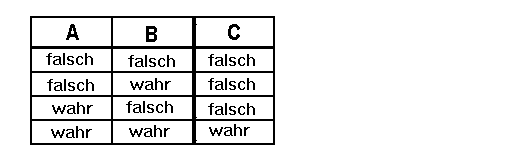 Diese W-Funktion hat nun einen besonderen Namen:
Man nennt sie UND-Funktion oder UND-Verknüpfung:
Der Name UND-Funktion rührt daher, daß sie genau dann
den Funktionswert "wahr" hat, wenn die Aussage A und
die Aussage B wahr ist.
Die UND-Verknüpfung ist die erste von vielen W-Funktionen
die wir kennenlernen werden.
Diese W-Funktion hat nun einen besonderen Namen:
Man nennt sie UND-Funktion oder UND-Verknüpfung:
Der Name UND-Funktion rührt daher, daß sie genau dann
den Funktionswert "wahr" hat, wenn die Aussage A und
die Aussage B wahr ist.
Die UND-Verknüpfung ist die erste von vielen W-Funktionen
die wir kennenlernen werden.
 Schreibweise
Werden zwei Variablen (x,y) durch eine "normale" Funktion
verknüpft, so gibt es dafür verschiedene Funktionen: + , - , · usw.
z= x+y oder z=x-y oder z=x·y
Auch zwei Aussagen kann man durch verschiedene W-Funktionen
verknüpfen. Verknüpft man die beiden Aussagen durch eine
UND-Funktion, so kürzt man dies mit dem Zeichen Schreibweise
Werden zwei Variablen (x,y) durch eine "normale" Funktion
verknüpft, so gibt es dafür verschiedene Funktionen: + , - , · usw.
z= x+y oder z=x-y oder z=x·y
Auch zwei Aussagen kann man durch verschiedene W-Funktionen
verknüpfen. Verknüpft man die beiden Aussagen durch eine
UND-Funktion, so kürzt man dies mit dem Zeichen 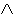 ab:
C = A ab:
C = A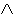 B
Bei W-Funktionen benutzt man allerdings nicht das Zeichen
= sondern das Zeichen B
Bei W-Funktionen benutzt man allerdings nicht das Zeichen
= sondern das Zeichen 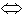 , um die Gleichheit auszudrücken:
C , um die Gleichheit auszudrücken:
C 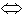 A A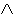 B
Das Zeichen B
Das Zeichen 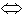 haben wir in Logik II kennengelernt. Es bedeutet
"hat den gleichen Wahrheitswert wie". Während man also bei
normalen Funktionen das Zeichen = benutzt, benutzt man bei
W-Funktionen das Zeichen haben wir in Logik II kennengelernt. Es bedeutet
"hat den gleichen Wahrheitswert wie". Während man also bei
normalen Funktionen das Zeichen = benutzt, benutzt man bei
W-Funktionen das Zeichen 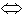 . .
|