21k1s0.htm Inhalt zu Matrizen I

Version 1 ©Raddy '99	Inhalt zu Matrizen I ZURÜCK
Info-Seite	Vorkenntnisse: .... Themen: ...... Infos: www.mathematik.net
Definition der Matrix	Eine Matrix ist ein rechteckiges Zahlenschema. Eine Matrix besteht aus waagerecht verlaufenden Zeilen und senkrechten verlaufenden Spalten: 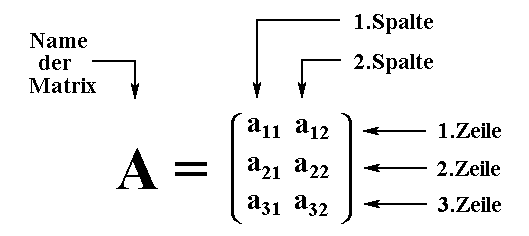Man sagt: Eine Matrix mit m Zeilen und n Spalten ist vom Typ (m,n).
Gleichheit von Matrizen	Zwei Matrizen sind gleich, wenn sie vom gleichen Typ sind und in jedem Element übereinstimmen
Zeilenmatrix Spaltenmatrix Nullmatrix	Zeilenmatrix: Eine Matrix, die aus nur einer Zeile besteht. Spaltenmatrix: Eine Matrix, die aus nur einer Spalte besteht. Nullmatrix: Eine Matrix, deren Elemente alle Nullen sind.
Zeilenvektor Spaltenvektor	Die Zeilen einer Matrix bezeichnet man auch als Zeilenvektoren. Die Spalten einer Matrix bezeichnet man auch als Spaltenvektoren.
Transponierte einer Matrix	Vertauscht man die Zeilen mit den Spalten einer Matrix A, so erhält man die transponierte Matrix A^T.
Quadratische Matrizen	Eine quadratische Matrix ist eine Matrix vom Typ (m,m):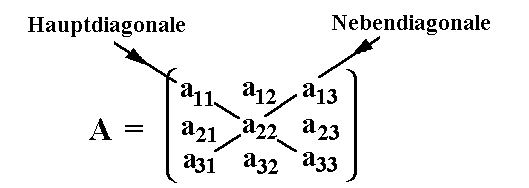
Diagonalmatrix Einheitsmatrix	Eine spezielle quadratische Matrix ist die Diagonalmatrix: Alle Elemente außerhalb der Hauptdiagonalen sind gleich Null. Eine spezielle Diagonalmatrix ist die Einheitsmatrix: Alle Elemente außerhalb der Hauptdiagonalen sind gleich Null. Die Elemente der Hauptdiagonalen sind gleich 1.
Dreiecksmatrizen	Zwei weitere Spezialfälle einer quadratischen Matrizen sind: Untere Dreiecksmatrix: Alle Elemente oberhalb der Hauptdiagonalen sind gleich 0. Obere Dreiecksmatrix: Alle Elemente unterhalb der Hauptdiagonalen sind gleich 0.
Symmetrische Matrix	Die symmetr.Matrix ist eine quadratische Matrix für die gilt: Je 2 Elemente, die spiegelbildlich zur Hauptdiagonalen liegen, sind gleich (a_ik=a_ki).
Schiefsymme- trische Matrix	1. Je zwei Elemente, die spiegelbildlich zur Hauptdiagonalen liegen, sind vom Betrag gleich, haben aber ein unterschiedliches Vorzeichen. 2. Die Elemente der Hauptdiagonalen sind gleich Null.