Verdeutlichung am Beispiel:
     
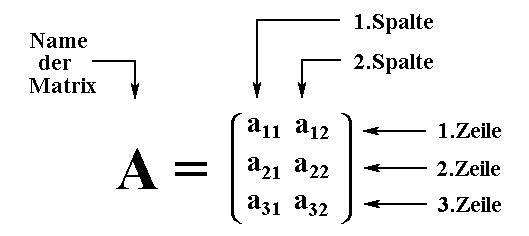
Anmerkungen zur Definition:
      Eine Matrix besteht aus reellen Zahlen, die man Elemente nennt.
           Z.B. sind die Elemente a₂₁ und a₂₂ Elemente der Matrix oben,
           genauer gesagt die Elemente der zweiten Zeile der Matrix.
          
      Eine Matrix wird in runde Klammern geschrieben.
          
      Eine Matrix wird mit einem großen Buchstaben bezeichnet,
          deren Elemente mit kleinen Buchstaben. Beispiel:
          Die Matrix A besteht aus den Elementen a₁₁, a₁₂,a₂₁, ...
         
      Anhand der Bezeichnung des Elementes kann man erkennen, zu
          welcher Matrix es gehört, am Index eines Elementes kann man
          erkennen, in welcher Zeile und Spalte das Element steht:
         
                 Z.B. ist das Element a₃₂ in der 3.Zeile und 2.Spalte der
                 Matrix A zu finden. Zweites Beispiel: Das Element c₉₇
                 steht in der 9.Zeile und 7.Spalte der Matrix C.

Weitere Bezeichnungen
      Für die Matrix A (siehe Bild) gibt es eine kürzere Schreibweise:
      A=(a_ik) mit 1<i<3 und 1<k<2. Oder noch kürzer: A=(a_ik)_(3,2).
      Allgemein schreibt man: A=(a_ik)_(m,n) für eine Matrix A
      mit m Zeilen und n Spalten, die aus den Elementen a_ik besteht.
Typ einer Matrix
      Hat eine Matrix m Zeilen und n Spalten, so sagt man, daß die Matrix
      vom Typ (m,n) ist. Z.B. ist die Matrix A (siehe Bild) vom Typ (3,2).