Transponierte
Matrix
|
 Definition:
Vertauscht man die Zeilen und die
Spalten einer Matrix A, so
heißt die enstandene Matrix die "Transponierte der Matrix A".
Die Transponierte der Matrix A nennt man AT . |
Beispiel:
Als Beispiel sei folgende Matrix vom Typ (3,2) gegeben:
Vertauchen wir nun die Zeilen und Spalten der Matrix, so
erhalten wir AT, d.h. die Transponierte der Matrix A:
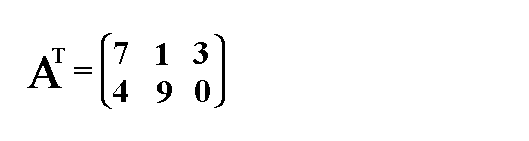
Anmerkungen zur Definition:
 Ist die Matrix A vom Typ (m,n), so ist die AT vom Typ (n,m)
 Transponiert man eine Matrix zweimal, so erhält man wieder
die ursprüngliche Matrix. Als Formel: (AT)T = A
 Die Elemente der Matrix A und der Matrix AT stehen
in folgenden Zusammenhang:
|
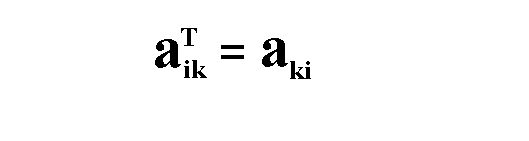