Schiefsymmetrische
Matrix |
 Definition: Definition:
Ein weiterer
Spezialfall der quadratischen Matrix ist die
sogenannte "schiefsymmetrische Matrix":
Eine "schiefsymmetrischen
Matrix" liegt vor, wenn gilt:
1. Die Elemente, die spiegelbildlich zur Hauptdiagonalen
liegen, sind vom Betrag gleich, haben aber entgegengesetzte
Vorzeichen.
2. Die Hauptdiagonalenelemente sind gleich Null.
Beide Teile der Definition kann man durch folgende Formel
zusammenfassen:
aik = -aki |
 Beispiele: Beispiele:
Folgende zwei
Matrizen sind schiefsymmetrische Matrizen:
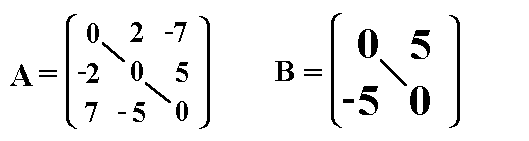
 Verständnisfrage: Verständnisfrage:
Warum würde die
Formel aik= -aki nicht mehr gültig sein,
wenn wir Teil 2 der Definition weglassen würden?
 Antwort: Antwort:
Gäbe es Teil 2 der
Definition nicht, so könnte in der Matrix A
ein Hauptdiagonalenelement (z.B. a33) einen Wert
ungleich Null
haben, also z.B. den Wert 9:
Schauen wir, ob die Formel aik= -aki
dann noch gelten würde:
aik
= -aki 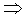 a33 = -a33 a33 = -a33
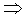 9 = -9 (falsch)
9 = -9 (falsch)
Da 9=-9 eine falsche Aussage ist, gilt die Formel aik=
-aki nicht mehr,
wenn man Teil 2 der Definiton fortfallen läßt.
 Transponieren einer schiefsymmetri.Matrix: Transponieren einer schiefsymmetri.Matrix:
Wird eine schiefsymmetrische Matrix A transponiert, so
ändern
sämtliche Matrixelemente ihr Vorzeichen (Am Bild
verdeutlichen!).
Wenn wir das nächste Kapitel (Matrizen II /
Skalar-Matrix-Produkt)
durchgearbeitet haben werden, werden wir diesen Satz
eleganter
formulieren können: Bei einer schiefsymmetrischen Matrix
gilt:
A =
-(AT)
|