Version 1 |
Inhalt zu Matrizen II ZURÜCK |
| Info-Seite | Vorkenntnisse: .... Themen: ...... Infos: www.mathematik.net |
| Addition von Matrizen |
Zwei
Matrizen werden elementweise addiert: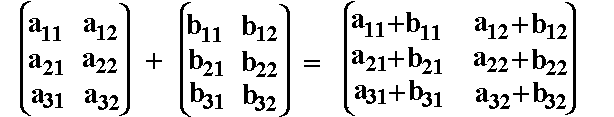  Die Matrizenaddition ist kommutativ und assoziativ. Sie ist nur
definiert, wenn beide Matrizen vom gleichem Typ sind. |
| Subtraktion von Matrizen |
Auch die
Subtraktion zweier Matrizen geschieht elementweise: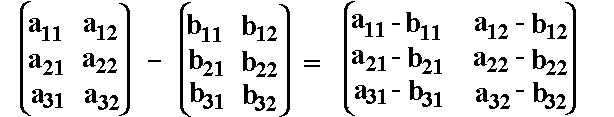 Die Matrizensubtraktion ist weder kommutativ noch
assoziativ. Sie ist nur
definiert, wenn beide Matrizen vom gleichem Typ sind. |
| Multiplikation eines Skalar mit einer Matrix |
Ein Skalar
(=reelle Zahl) wird mit einer Matrix multipliziert, indem man jedes Element der Matrix mit dem Skalar multipliziert: 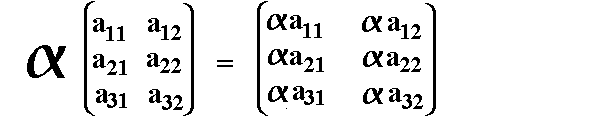 Die
Skalar-Matrix-Multiplikation ist assoziativ und distributiv. |
| Matrizenprodukt | Zwei
Matrizen A und B werden multipliziert, indem man jeder Zeilenvektor der Matrix A mit jedem Spaltenvektor von B multipliziert wird:  |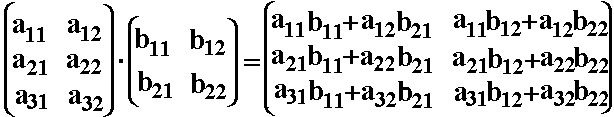
| Anmerkungen zum Matrizenprodukt |
Das
Matrizenprodukt A·B ist nur definiert, wenn die Spaltenzahl von A mit der Zeilenzahl von B übereinstimmt. Die Matrix
C=A·B hat soviele Zeilen wie A Zeilen hat.Die Matrix C=A·B hat soviele Spalten wie B Spalten hat. |
| Beispiel zum Matrizenprodukt |
Ein Beispiel: Das Produkt zweier (2,2) Matrizen ist zu bilden ..... |
| Schema zum Matrizenprodukt |
Die
Matrizenmultiplikation gestaltet sich besonders einfach, wenn man sie nach einem besonderen Schema ausführt. Das Schema geht so ..... |
| Gesetze des Matrizenprodukt |
Kommutativgesetz:
nein, gilt im Allgemeinen nicht Assoziativgesetz: (AB)C = A(BC) Distributivgesetze: A(B+C) = AB + AC (A+B)C = AC + BC |