Version 1
©Raddy '99		 Matrizen II                               ZURÜCK 
Multiplikation
eines Skalar mit
einer Matrix
 
a-absatz.pcx (280 Byte)Definition
Ein Skalar 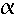a-g-alpa.pcx (200 Byte) (eine Zahl) wird mit einer Matrix A multipliziert,
indem man jedes Matrixelement mit dem Skalar multipliziert.		 


a-absatz.pcx (280 Byte)Gesetze  
      Für die Skalar-Matrix-Multiplikation gelten folgende Gesetze:

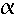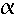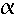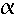      Assoziativgesetz:    a-g-alpa.pcx (200 Byte)1(a-g-alpa.pcx (200 Byte)2A) = (a-g-alpa.pcx (200 Byte)1a-g-alpa.pcx (200 Byte)2)A 
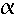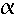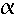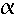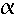      Distributivgesetze:  (a-g-alpa.pcx (200 Byte)1+a-g-alpa.pcx (200 Byte)2)A = a-g-alpa.pcx (200 Byte)1A+a-g-alpa.pcx (200 Byte)2A
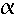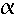                                        a-g-alpa.pcx (200 Byte)1(A+B) = a-g-alpa.pcx (200 Byte)1A + a-g-alpa.pcx (200 Byte)1B
       
a-absatz.pcx (280 Byte)Beispiel
     
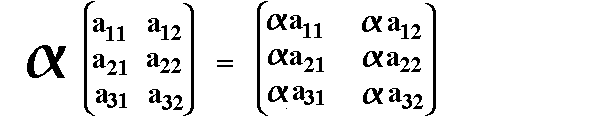
     21k1s3p1.pcx (7325 Byte)
      
      
a-absatz.pcx (280 Byte)Anmerkungen 
      (1) Das Beispiel bzw. die Definition kann man auch anders herum lesen: 
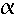            Ein Faktor a-g-alpa.pcx (200 Byte) der in allen Elementen einer Matrix enthalten ist, 
            darf vor die Matrix geschrieben werden. 
      (2) Den "Multiplikationspunkt" haben wir, so wie es üblich ist, fortgelassen,
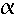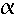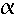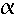            z.B. müßte man für a-g-alpa.pcx (200 Byte)1(a-g-alpa.pcx (200 Byte)2A) genaugenommen a-g-alpa.pcx (200 Byte)1·(a-g-alpa.pcx (200 Byte)2·A) schreiben.