Beispiel 

Beispiel 
       Gegeben seien die Matrizen A und B, gesucht das Matrizenprodukt C=A·B
     
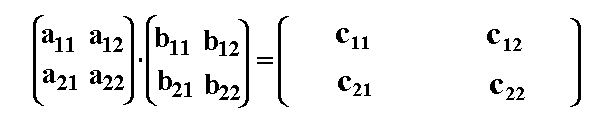
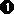       Als erstes werden wir das Element c11 berechnen. Laut Definition gilt:
           c11 ist gleich dem Skalarprodukt aus dem 1.Zeilenvektor der Matrix A
           und dem 1.Spaltenvektor der Matrix B: 
          
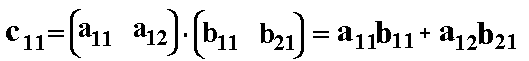           Jetzt tragen wir c11 in die Ergebnismatrix ein:
      
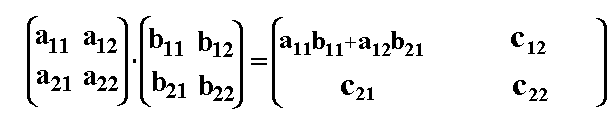
       Analog berechnen wir das Element c12 der Ergebnismatrix: Laut
           Definition ist c12 gleich dem Skalarprodukt aus dem 1.Zeilenvektor 
           der Matrix A und dem 2.Spaltenvektor der Matrix B:
           
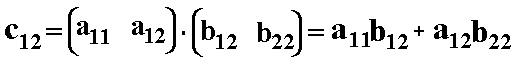           Auch c12 tragen wir in die Ergebnismatrix ein:
      
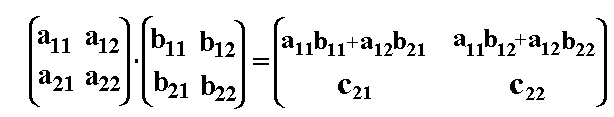
       Schließlich müssen wir nur noch die Elemente c21 und c22 berechnen:
            c21 ist das Skalarprodukt aus dem 2.Zeilenvektor der Matrix A und 
            dem 1.Spaltenvektor der Matrix B.
            c22 ist das Skalarprodukt aus dem 2.Zeilenvektor der Matrix A und 
            dem 2.Spaltenvektor der Matrix B.
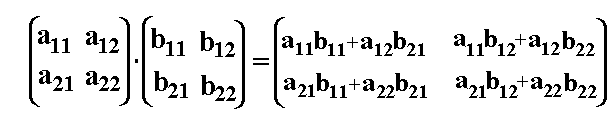