Multiplikation
zweier Matrizen
|
 Definition
Das Produkt einer Matrix A=(aik)
mit einer Matrix B=(bik) ist
ebenfalls eine Matrix, die wir Matrix C=(cik) nennen.
Die Elemente cik der Matrix C werden auf folgende Weise
gebildet:
Das Element cik ist das Skalarprodukt des i-ten Zeilenvektors
der Matrix A mit dem k-ten Spaltenvektor der Matrix B. |
Beispiel
Gegeben sei eine Matrix A=(aik) und eine Matrix B=(bik). Das Produkt
der beiden Matrizen ist laut Definition wieder eine Matrix, die wir in
der Definition C=(cik) genannt hatten:
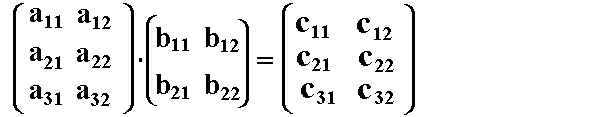Warum die Matrix C vom Typ (3,2) ist wird erst auf der nächsten Seite
erklärt. Jetzt wollen wir die Matrix erst einmal berechnen:
Um die Matrix C zu bestimmen muß man nun (mit Hilfe der Definition)
deren Elemente cik bestimmen. Exemplarisch bestimmen wir c32:
Laut Definition ist c32 gleich dem Skalarprodukt aus dem 3.Zeilenvektor
der Matrix A und dem 2.Spaltenvektor der Matrix B:
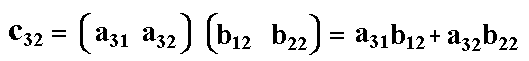Nun können wir das Element c32 in die Matrix C eintragen:
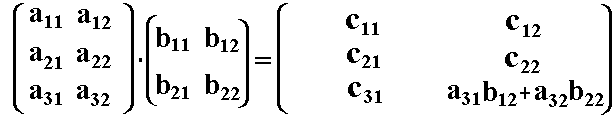Die Berechnung der restlichen Elemente (c11, c12, c21, c22 und c31)
erfolgt analog. Das Ergebnis lautet:
|
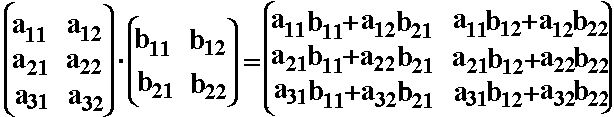