Anmerkungen zum
Matrizenprodukt
|
 Anmerkung 1 Anmerkung 1
Das Matrizenprodukt A·B ist nur
definiert, wenn die Spaltenzahl
der Matrix A mit der Zeilenzahl der Matrix B übereinstimmt. |
Man sagt auch: Ist eine Matrix A vom Typ (m,n) so kann sie nur dann mit
einer Matrix B multipliziert werden, wenn die Matrix B vom Typ (n,r) ist.
Erklärung: Nehmen wir an, die Spaltenzahl der Matrix A würde nicht mit
der Zeilenzahl der Matrix B übereinstimmen, sondern wäre z.B. kleiner:
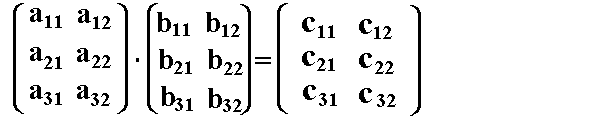 Nun berechnen wir z.B. c11. Laut Definition ist c11 gleich dem Skalarprodukt
aus dem 1.Zeilenvektor von A und dem 1.Spaltenvektor von B.
Nun berechnen wir z.B. c11. Laut Definition ist c11 gleich dem Skalarprodukt
aus dem 1.Zeilenvektor von A und dem 1.Spaltenvektor von B.
(a11, a12)·(b11, b21, b31)
Dieses Skalarprodukt ist aber gar nicht definiert. Das Skalarprodukt ist
nämlich nur zwischen Vektoren definiert, die gleich viele Komponenten haben.
Ist das Skalarprodukt nicht definiert, so gilt dies auch für das Matrizenprodukt.
 Anmerkung 2 Anmerkung 2
Die Matrix C=A·B hat soviele Zeilen
wie die Matrix A und
soviele Spalten wie die Matrix B. |
Man sagt auch: Ist die Matrix A vom Typ (m,n) und B vom Typ (n,r),
so ist die Matrix C vom Typ (m,r).
Warum ist das so? Wir erklären dies am Beispiel der Vorseite.
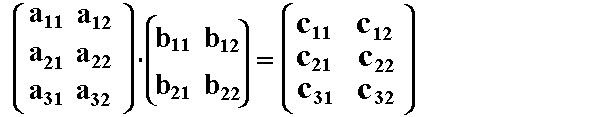 Laut obrigen Satz hat die Matrix C genau 3 Zeilen.
Nun beweisen wir, daß die Matrix C keine 4 Zeilen haben kann:
Nehmen wir an, die Matrix C hätte 4 Zeilen, dann gäbe es z.B.
ein Element c41. Dieses wäre definiert als das Skalarprodukt
aus dem 4.Zeilenvektor von A und dem 1.Spaltenvektor von B.
Da die Matrix A aber keinen 4.Zeilenvektor hat, kann man kein
Element c41 bilden, und somit hat die Matrix C keine 4 Zeilen.
Laut obrigen Satz hat die Matrix C genau 3 Zeilen.
Nun beweisen wir, daß die Matrix C keine 4 Zeilen haben kann:
Nehmen wir an, die Matrix C hätte 4 Zeilen, dann gäbe es z.B.
ein Element c41. Dieses wäre definiert als das Skalarprodukt
aus dem 4.Zeilenvektor von A und dem 1.Spaltenvektor von B.
Da die Matrix A aber keinen 4.Zeilenvektor hat, kann man kein
Element c41 bilden, und somit hat die Matrix C keine 4 Zeilen.
|
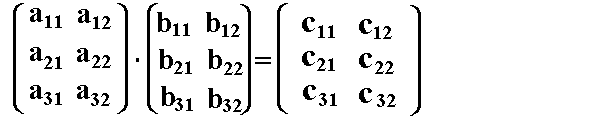 Nun berechnen wir z.B. c11. Laut Definition ist c11 gleich dem Skalarprodukt
aus dem 1.Zeilenvektor von A und dem 1.Spaltenvektor von B.
Nun berechnen wir z.B. c11. Laut Definition ist c11 gleich dem Skalarprodukt
aus dem 1.Zeilenvektor von A und dem 1.Spaltenvektor von B. 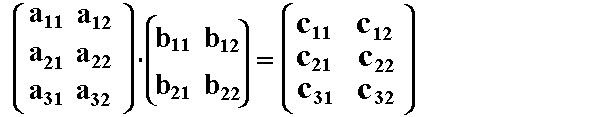 Laut obrigen Satz hat die Matrix C genau 3 Zeilen.
Nun beweisen wir, daß die Matrix C keine 4 Zeilen haben kann:
Nehmen wir an, die Matrix C hätte 4 Zeilen, dann gäbe es z.B.
ein Element c41. Dieses wäre definiert als das Skalarprodukt
aus dem 4.Zeilenvektor von A und dem 1.Spaltenvektor von B.
Da die Matrix A aber keinen 4.Zeilenvektor hat, kann man kein
Element c41 bilden, und somit hat die Matrix C keine 4 Zeilen.
Laut obrigen Satz hat die Matrix C genau 3 Zeilen.
Nun beweisen wir, daß die Matrix C keine 4 Zeilen haben kann:
Nehmen wir an, die Matrix C hätte 4 Zeilen, dann gäbe es z.B.
ein Element c41. Dieses wäre definiert als das Skalarprodukt
aus dem 4.Zeilenvektor von A und dem 1.Spaltenvektor von B.
Da die Matrix A aber keinen 4.Zeilenvektor hat, kann man kein
Element c41 bilden, und somit hat die Matrix C keine 4 Zeilen.