Einleitung
Als zweites Beispiel in diesem Kapitel wollen wir die Folge
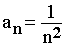 untersuchen, d.h. wir wollen beweisen, daß
sie eine Nullfolge ist. Der Beweis verläuft analog zum  
vorigen Beispiel, und kann deshalb übersprungen werden.
    

Lösung

Wir müssen also untersuchen, ob gilt:
 
        für beliebig kleine 

Die Betragstriche dürfen wir weglassen, denn der Term
auf der linken Seite ist immer positiv: 

         
Nun können wir die Formel nach n umstellen:
Wir multiplizieren mit n² und dividieren durch :

        

Jetzt müssen wir nur noch die Wurzel ziehen:

          

Wir fassen den Beweis zusammen:



Da es zu jedem noch so kleinem  eine Zahl n gibt, ab der
alle Glieder der Folge kleiner als  sind, ist die Folge eine
Nullfolge.