|
Folgende Gleichung soll
gelöst werden:
 x4+2x3+x2 = 0
x4+2x3+x2 = 0
Nun wird x ausgeklammert, daß heißt die Gleichung
wird faktorisiert (in Faktoren zerlegt):
 x2·(x2+2x+1) = 0
x2·(x2+2x+1) = 0
Eine erste Lösung der Gleichung muß x=0 sein, denn setzt
man 0 in die faktorisierte Gleichung ( ) ein, so wird der ) ein, so wird der
linke Faktor auf jeden Fall 0, und somit die Gleichung wahr:
 02·(x2+2x+1) = 0
02·(x2+2x+1) = 0
Weitere Lösung(en) ergeben sich, wenn die Klammer der
faktorisierten Gleichung (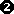 ) gleich Null wird: ) gleich Null wird:
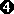 (x2+2x+1) = 0
(x2+2x+1) = 0
Diese quadratische Gleichung löst man mit der uns bereits
bekannten "Lösungsformel für quadratische Gleichungen",
bzw. hier mit der 1.binomischen Formel, und erhält -1 als
eine weitere Lösung.
Diese Lösung ist eine weitere Lösung der ursprünglichen
Gleichung. Die ursprüngliche Gleichung (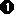 ) hat also ) hat also
die Lösungen 0 und -1. |