|
Folgende Gleichung soll
gelöst werden:
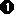 x5–6x3+9x = 0
x5–6x3+9x = 0
Weil kein Absolutglied vorhanden ist, können wir x
ausklammern:
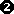 x·(x4–6x2+9) = 0
x·(x4–6x2+9) = 0
Daraus ergibt sich die 1.Lösung der Gleichung x=0, denn
für x = 0 wird die ganze linke Seite der Gleichung gleich 0,
und somit wird die Gleichung wahr.
Die anderen Lösungen der Gleichung 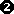 erhält man, erhält man,
wenn die Klammer gleich 0 wird, d.h. wir müssen
folgende Gleichung lösen:
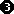 x4–6x2+9 = 0
x4–6x2+9 = 0
Wir führen nun eine Substitution durch: x2 = z
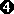 z2–6z+9 = 0
z2–6z+9 = 0
Diese quadratische Gleichung lösen wir im allgemeinen
mit der Lösungsformel für quadratische Gleichungen. Da
hier jedoch das 2.Binom vorliegt, dürfen wir schreiben:
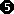 (z–3)2 =0
=> z=3
(z–3)2 =0
=> z=3
Die Rücksubstitution z=x2 ergibt die Gleichung
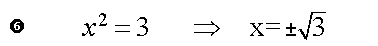
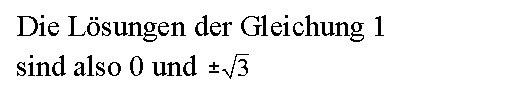 |