|
Als Beispiel wollen wir
folgende Funktion betrachten:
f(x) = x3+x2+x+1
Nun machen wir eine Tabelle, und tragen den Funktionswert
für verschiedene x ein. Dahinter schreiben wir die
Funktionswerte der einzelnen Glieder:
x |
f(x) |
x3 |
x2 |
x |
1 |
| 1 |
4 |
1 |
1 |
1 |
1 |
| 10 |
1111 |
1000 |
100 |
10 |
1 |
| 100 |
1.010.101 |
1.000.000 |
10.000 |
100 |
1 |
| 1000 |
1.001.001.001 |
1.000.000.000 |
1.000.000 |
1000 |
1 |
Wir bemerken folgendes:
Je größter x ist, desto mehr hängt der
gesamte
Funktionswert f(x) vom größten Glied (x3)
ab.
z.B. machen für x=1000 die Glieder x2+x+1 zusammen nur
noch 1% des gesamten Funktionswertes aus, x3 aber rund 99%.
Der Funktionsgrad verläuft der Graph also ungefähr so,
wie die Potenzfunktion g(x) = x3 verlaufen würde. Die
Verallgemeinerung dieser Aussage halten wir in einem Satz fest:
Gegeben sei ein ganzrationale Funktion:
f(x) = anxn
+ an-1xn-1 + ... + a1x + a0
(an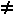 0) 0)
Dann verläuft ihr Graph für große |x| ungefähr so,
wie der Graph des größten des Gliedes, d.h. wie:
g(x) = anxn |
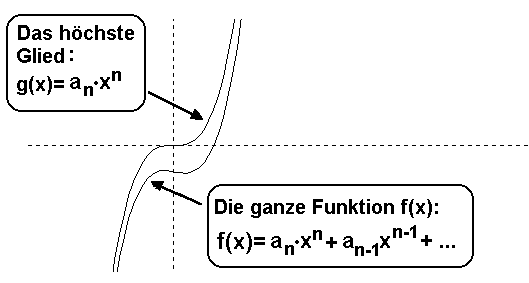
Das Bild zeigt eine ganzrationale
Funktion f(x) dritten Grades,
die für große |x| so verläuft, wie ihr größtes Glied g(x):
 |