|
Wir haben gesagt, daß eine
ganzrationale Funktion im
Unendlichen so verläuft wie ihr größtes Glied. Deshalb
wird eine ganzrationale Funktion mit geraden Exponenten
entweder von links oben nach rechts oben verlaufen, oder
aber von links unten nach rechts unten:
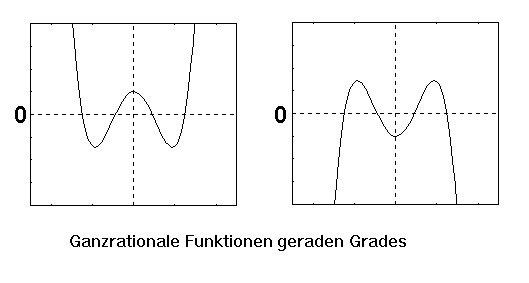
Wie man sieht wird im Beispiel oben die x-Achse viermal
geschnitten, d.h. die Funktionen haben beide 4 Nullstellen.
Das untere Bild zeigt aber, daß manche geraden Funktion die x-Achse garnicht berühren,
und somit garkeine Nullstelle haben:
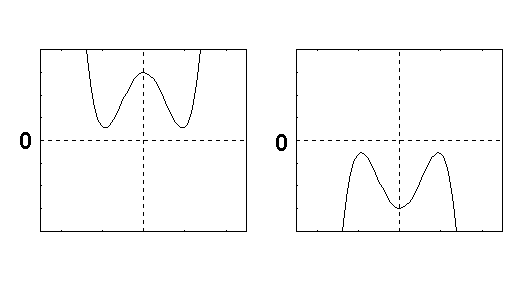
Eine ganzrationale Funktion mit geraden
Grad kann keine Nullstelle haben. |
|