Mindestzahl
Nullstellen
bei Funktion
mit ungeraden
Grad |
 |
Einleitung |
|
Nun wollen wir uns
überlegen, wieviele Nullstellen
eine ganzrationale Funktion mindestens hat.
Auf dieser Seite betrachten wir erstmal die ganzrationalen Funktionen mit ungeraden
Grad, wie z.B. f(x)= x3-2x2+3
|
 |
Ganzrat.Funktion
mit ungeraden Grad |
|
Wir haben gesagt, daß
ganzrationale Funktion im Unendlichen
so verlaufen wie ihr größtes Glied, also wie eine Potenzfunktion.
Deshalb wird eine ganzrationale Funktion mit ungeraden
Exponenten entweder von links unten nach rechts oben verlaufen,
oder aber von links oben nach rechts unten. Beispiel:
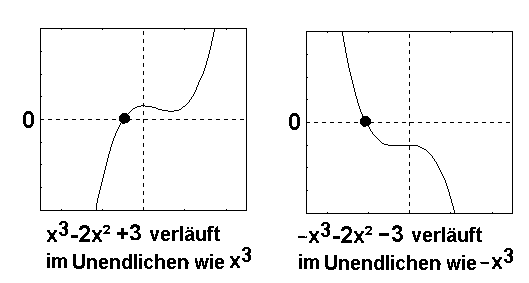
Wie man sieht, wird dabei die x-Achse mindestens einmal
durchkreuzt. Eine ganzrationale Funktion mit ungeraden Grad
wird somit mindestens eine Nullstelle haben:
Eine ganzrationale Funktion mit ungeraden
Grad hat mindestens eine Nullstelle. |
© by www.mathematik.net |
|