|
Im folgenden
betrachten wir die Funktion: f(x)=3x3-9x+6 :
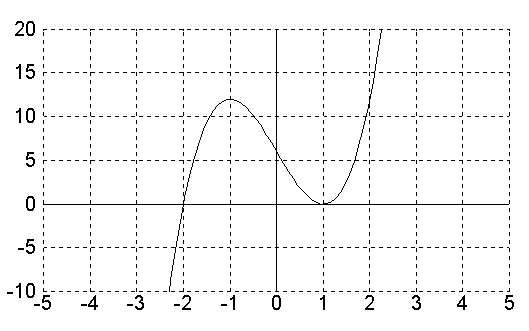
Die Nullstellen sind die Lösungen der zugehörigen Polynomgleichung:
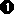 3x3–9x+6 = 0
3x3–9x+6 = 0
Wir versuchen eine erste Lösung durch Raten zu finden, und
beginnen wie immer unter den Teilern des Absolutgliedes.
Wir erraten die Lösung x1=
1 . Weil x=1 eine Lösung ist,
dürfen wir den Linearfaktor (x-1) abspalten:
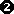 (3x3-9x+6) = (x-1)·(3x2+3x-6)
(3x3-9x+6) = (x-1)·(3x2+3x-6)
Die rechte Klammer von 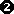 ist eine quadratische Funktion.
ist eine quadratische Funktion.
Wir bilden ihre Normalform, indem wir 3 ausklammern:
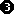 (3x3-9x+6) = 3(x-1)(x2+x-2)
(3x3-9x+6) = 3(x-1)(x2+x-2)
Die weiteren Nullstellen der Funktion f(x) sind die Nullstellen
der quadratischen Funktion in der rechten Klammer von 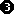 , ,
die man am besten mit der pq-Formel löst. Man erhält:
x2=1 und x3= -2
Nun benutzen wir den Satz von Vieta (für quadratische
Funktionen),
und zerlegen damit die quadratische Funktion,
die in der rechten
Klammer von 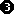 steht: steht:
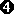 (3x3-9x+6) = 3(x-1)(x-1)(x+2)
(3x3-9x+6) = 3(x-1)(x-1)(x+2)
Hier tritt nun der interessante Fall ein, daß der Linearfaktor (x-1) doppelt auftritt,
also die Nullstelle x=1 doppelt vorhanden ist.
Auf der folgenden Seite untersuchen wir den Graph an der
einfachen und an der doppelten Nullstelle. |