Sonderfälle:
1n
0n
00
a1
a0 |
|
Die Zahl 1 nimmt eine
Sonderstellung bezüglich des Potenzierens ein:
So oft man die Zahl 1 mit sich selbst multipliziert, es wird immer die
Zahl 1 herauskommen:
1 · 1 · 1 · .... · 1 = 1
Deshalb gilt: |
|
Eine ähnliche Sonderstellung
(bezüglich des Potenzierens) nimmt
die Zahl 0 ein: So oft man die Zahl 0 mit sich selbst multipliziert,
es wird immer die Zahl 0 herauskommen:
0 · 0 · 0 · .... · 0 = 0
Deshalb gilt: |
|
Die Potenz 00 ist nicht
definiert (ähnlich wie a:0 nicht definiert ist).
Da wir Exponenten aus Z erst im Kapitel 2 kennen lernen, werden wir
auch den Beweis des Satzes erst dort erbringen. Wir merken uns aber: |
|
Auf diesen Sonderfall hatten wir
schon in der Definition der Potenz
hingewiesen, der Beweis folgt in diesem Kapitel. Wir merken uns: |
|
Potenzen der Form a0
haben der Wert 1.
Da wir Exponenten aus Z erst im Kapitel 2 kennen lernen, werden wir
auch den Beweis des Satzes erst dort erbringen. Wir merken uns aber:
a0 = 1 mit: a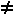 0 0 |
Wir müssen dabei a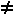 0 fordern, denn oben haben wir ja
gesagt, 0 fordern, denn oben haben wir ja
gesagt,
daß 00 nicht definiert ist. |
|