Erweiterung
der Potenzgesetze
für negative
Exponenten |
 |
Einleitung |
|
Potenzgesetz 1b lautete:
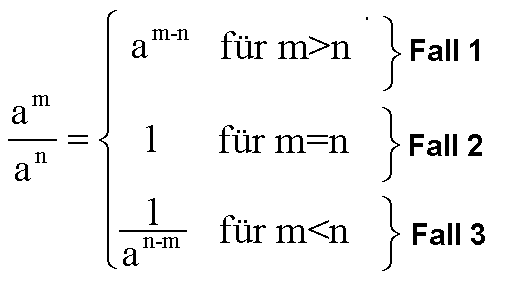
Nachdem wir auf der vorletzten Seite die Fallunterscheidung
für Fall 2 überflüssig gemacht haben, wollen wir nun die
Fallunterscheidung für Fall 3 (siehe Bild) überflüssig machen.
Dazu wollen wir eine Division wie in Fall 3 durchführen:

Wir führen diese Division auf zwei Arten durch, im Bild links
nach der Formel für Fall 1, und rechts nach der Formel für Fall 3:
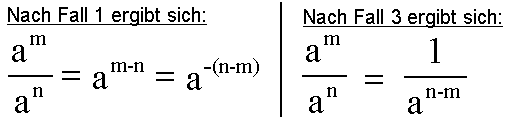
Falls Du die Umstellung im linken Bild nicht verstehst: Der Exponent
(m-n) wurde durch Ausklammern von -1 zum Exponenten -(n-m).
Durch Gleichsetzen der Ergebnisse erhalten wir:
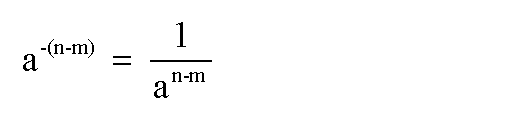
Laut Voraussetzung ist n>m, also ist (n-m) eine natürliche Zahl.
Dieser natürlichen Zahl (n-m) geben wir den Namen b:

Durch diese Formel haben wir eine wichtige Regel aufgestellt,
die angibt wie man einen negativen Exponenten zu verstehen hat:
Eine Potenz mit negativen Exponenten ist gleich dem Kehrwert
der Potenz mit positiven Exponenten. |
|