| Satz über Potenzen mit negativen Exponenten |
 |
Satz |
|
Wir haben gerade erfahren, wie ein negativer
Exponent
zu verstehen ist:

Der Exponent einer Potenz wechselt das Vorzeichen,
wenn man den Kehrwert der Potenz bildet.
Nun leiten wir daraus eine weitere Definition für "Potenzen
mit negativen Exponenten" ab:
Der Exponent einer Potenz wechselt das Vorzeichen,
wenn man den Kehrwert der Basis bildet:
 |
 |
Beweis für rationale Basis (Brüche): |
|
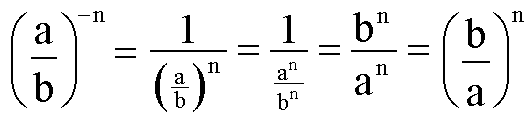
1.Zuerst bilden wir ganz normal den Kehrwert der
gesamten Potenz.
2.Nun ist der Exponent eine natürliche Zahl, und wir können
das Potenzgesetz 2b aus Kapitel 2 anwenden.
3.Den Doppelbruch mit bn erweitern.
4.Nun nochmal das Potenzgesetz 2b aus Kapitel 2 anwenden.
|
 |
Beweis für ganzzahlige Basis |
|
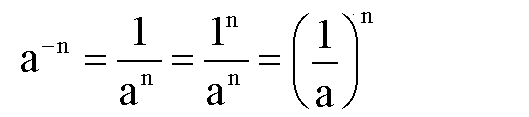
1.Zuerst bilden wir ganz normal den Kehrwert der
gesamten Potenz.
2.Weil 1n=1 , dürfen wir im Zähler 1n schreiben.
3.Nun nochmal das Potenzgesetz 2b aus Kapitel 2 anwenden. |
|