Beweis des
Potenzgesetz
1b / Fall 2 |
 |
Fall 2: Einer der Exponenten ist negativ |
|
Wir wollen das Potenzgesetz 1b für ganzzahlige
Exponenten
beweisen, und zwar den Fall, daß einer der Exponenten negativ
ist. Als Beispiel sei der zweite Exponent (also s) negativ:
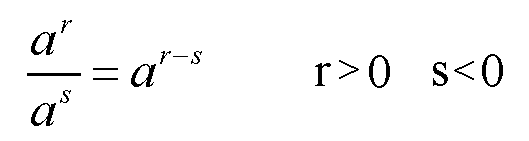
Weil s laut Voraussetzung negativ ist, dürfen wir schreiben:
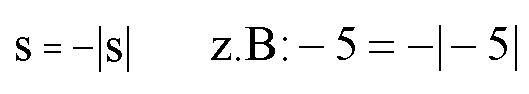
Eingesetzt in die erste Gleichung (linke Seite) ergibt sich:

Nun wenden wir auf den Nenner die Definition von Potenzen mit
negativen Exponenten an: Wenn man den Kehrwert der Potenz
bildet, wechselt der Exponent sein Vorzeichen:

Aus der Bruchrechnung wissen wir: Eine Zahl wird durch einen
Bruch dividiert, indem man die Zahl mit den dem Kehrwert des
Nenners multipliziert:

Weil beide Potenzen positive Exponenten haben (Beträge sind ja
immer positiv) dürfen wir das (alte) Potenzgesetz für natürliche
Exponenten anwenden, und erhalten:

Am Anfang des Beweises hatten wir s ersetzt: s=-|s|
Wir formen diese Gleichung um: s=-|s| 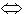 -s=|s| -s=|s|
Wir dürfen also |s| durch -s ersetzen, und erhalten:
 |
|