Beweis des
Potenzgesetz
3 / Fall 2 |
 |
Beweis des Potenzgesetz 3 / Fall 2 |
|
Wir wollen das Potenzgesetz 3 für ganzzahlige
Exponenten
beweisen. Wir betrachten den Fall 2, bei dem beide Exponenten
(r und s) negativ sein sind:
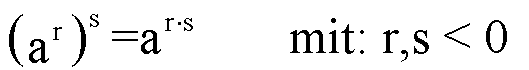
Weil r,s laut Voraussetzung negativ sind, dürfen wir schreiben:
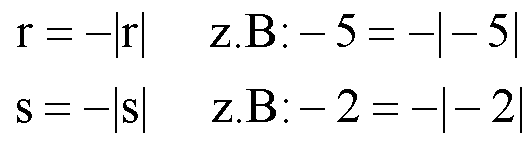
Eingesetzt in die erste Gleichung (linke Seite) ergibt sich:

Nun wenden wir zweimal die Definition von Potenzen mit
negativen Exponenten an: Wenn man den Kehrwert der Potenz
bildet, wechselt der Exponent sein Vorzeichen:

Doppelbruch mit a|r| erweitern, Nenner wird dadurch zu 1:

Weil beide Potenzen den positive Exponenten r haben (Beträge
sind ja immer positiv) dürfen wir das (alte) 3.Potenzgesetz für
natürliche Exponenten anwenden, und erhalten:

Wir haben ganz oben bewiesen: r = -|r| . Daraus
folgt: -r = |r|
Genauso folgt: -s = |s| , und wir erhalten:
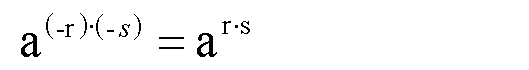 |
|