2. Erweiterung der Potenzdefinition:
Erweiterung
auf rationale
Exponenten |
 |
Die 2.Erweiterung der Potenzdefinition |
|
Nun stellt sich erstens die Frage ob es einen
Grund geben könnte,
die Potenzdefinition nochmals zu erweitern. Zweitens stellt sich die Frage,
wie diese Erweiterung der Potenzdefinition lauten könnte.
Dazu wiederholen wir zunächst das Kürzen
von Wurzelexponenten
(neues Browser-Fenster) an einem Beispiel:
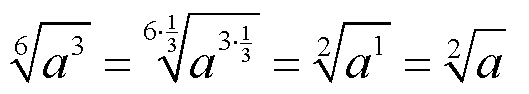
Nun schauen wir was passiert, wenn wir den Wurzelexponenten
kürzen, obwohl Wurzelexponent und Exponent teilerfremd sind, und
der Wurzelexponent so gekürzt wird, daß er "1" wird und wegfällt:
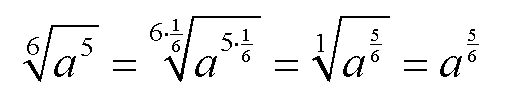
Diese Gleichung beantwortet die zwei oben gestellten Fragen:
 Es ist notwendig zu
definieren, was man unter einem rationalen
Exponenten versteht, da diese beim Kürzen auftreten können.
 Schreiben wir die
zweite Gleichung allgemein auf, dann liefert
sie uns bereits die gesuchte Definition, also die Definition
von Potenzen mit rationalen Exponenten:
Natürlich müssen wir noch beweisen, daß die Potenzgesetze
auch für rationale Exponenten gültig bleiben!
Die ausführlichen Beweise finden sich am Ende des Kapitels,
sind aber nicht unbedingt zum Verständnis erforderlich.
© www.mathematik.net |
|