Anmerkungen zur
2.Erweiterung der
Potenzdefinition: |
 |
Negative Basen sind verboten ! |
|
Im Kapitel Wurzeln lernten wir, daß der
Radikand einer Wurzel
nicht negativ sein darf, denn dann wäre die Wurzel nicht definiert.
Nun haben wir aber gerade gelernt, daß Potenzen mit rationalen
Exponenten ebenfalls Wurzeln sind (siehe Gleichung).
Für die Basis a einer Potenz mit rationalen Exponenten heißt dies,
daß man nur eine nichtnegative Basen a zulassen darf, denn sonst könnte
der zugehörige Radikand negativ werden (d.h. Wurzel nicht definiert):
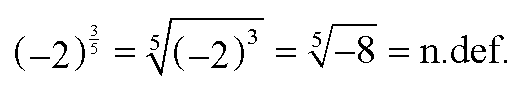
Aber auch die Zahl 0 müssen wir als Basis
ausschließen. Dies ist zwar bei
positiven rationalen kein Problem, aber bei negativen Zahlen gibt es ein Problem:
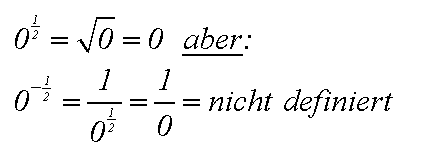
|
 |
Minus im Nenner des Exponenten |
|
Bei rationalen Exponenten stellt sich die Frage,
was man macht,
wenn im Nenner des Exponenten eine negative Zahl steht.
In diesem Fall wäre der Wurzelexponent (-2) negativ, und
sowas haben wir im Kurs Wurzelrechnung nicht definiert:
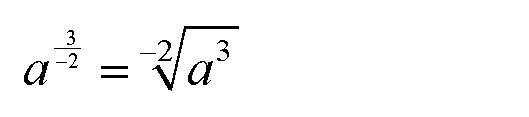
Natürlich kann man in diesem Fall das Vorzeichen in den
Zähler bringen, und schon ist das Problem gelöst:
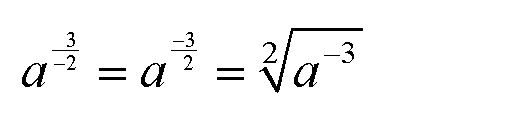
|
 |
Exponent ist Dezimalzahl |
|
Auch eine Dezimalzahl im Exponenten stellt kein
Problem dar.
Schließlich kann man ja jede Dezimalzahl in einen Bruch
verwandeln:
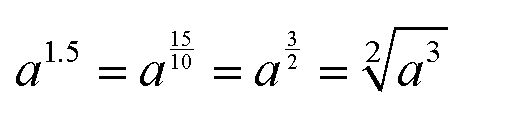
|
|