| Beweis des Potenzgesetz 2a (für rationale
Exponenten) |
 |
Beweis Potenzgesetz 2a |
|
Wir wollen das Potenzgesetz 2a für rationale
Exponenten beweisen:
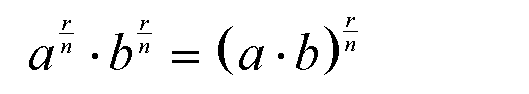
Aus dem Kurs Wurzelrechnung wissen wir: Wir dürfen einen
Term mit einer Zahl n potenzieren, wenn wir anschließend mit n
Radizieren, denn Potenzieren und Radizieren heben sich dann auf.
Deshalb dürfen wir jeden Faktor auf der linken Seite der
Gleichung mit n potenzieren und radizieren:
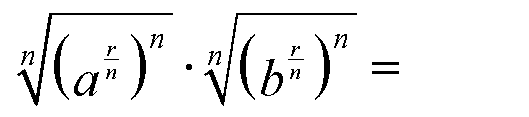
Potenzgesetz 3 für rationale Exponenten anwenden:
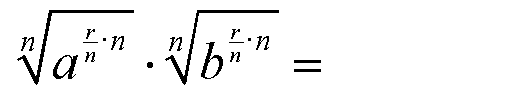
In beiden Exponenten kann n gekürzt werden:
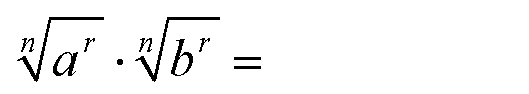
Das Wurzelgesetz 1 anwenden:
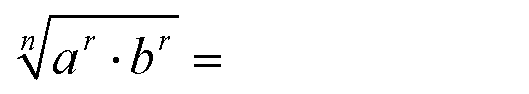
Das (alte) Potenzgesetz 2a für ganzahlige Exponenten nutzen:
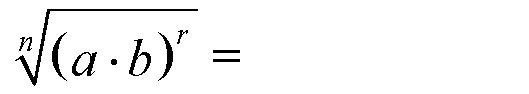
Potenzdefinition für rationale Exponenten anwenden:

|
|