Wir wollen das Potenzgesetz
2b für rationale Exponenten beweisen:
|
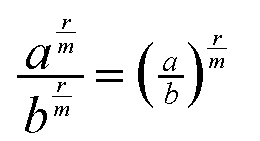 |
Zuerst wird sowohl der Zähler als auch der Nenner mit m
potenziert und dann die m-te Wurzel gebildet.
Weil sich Potenzieren und Wurzelziehen aufheben dürfen wir dies tun: |
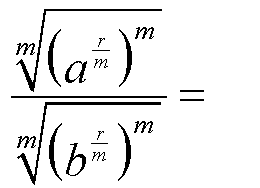 |
| Nun wird das 3.Potenzgesetz für rationale Exponenten auf
die Exponenten im Zähler bzw. im Nenner angewendet: |
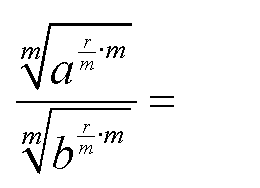 |
| Jetzt wird im Zähler und Nenner mit m gekürzt: |
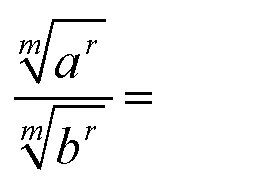 |
| Dann wird das 2.Wurzelgesetz angewendet: |
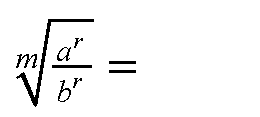 |
| Jetzt wird auf den Radikand das Potenzgesetz 2b angewendet: |
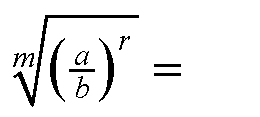 |
| Schließlich wird wieder die "Definition einer Potenz
mit rationalen Exponenten" angewendet: |
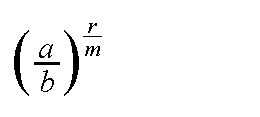 |