Exponent ist ungerade,
Konstante ist negativ |
 |
Worum geht es? |
|
Es geht nun um den Fall, dass auf der einen Seite eine ungerade Potenz
steht (hier: x3), und auf der anderen Seite eine
negative Konstante (hier: –8):
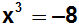
|
 |
Lösungsweg |
|
|
Lösungsweg: |
Beispiel |
| Gegebene Gleichung: |
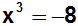 |
Würden wir jetzt beide Seiten radizieren, dann
stände
auf der rechten Seite der Gleichung der undefinierte
Ausdruck:

Wir machen daher einen Trick, und quadrieren
beide Seiten: |
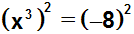 |
Auf der linken Seite wenden wir das folgende
Potenzgesetz an:
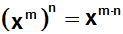 |
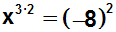 |
Beide Seiten vereinfachen. Wir erhalten eine
Potenzgleichung mit geradem Exponenten. |
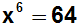 |
Wir lösen die Potenzgleichung mit geradem
Exponenten wie üblich: Zuerst beide Seiten
mit dem Exponenten (hier: 6) radizieren: |
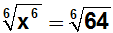 |
Jetzt wenden wir das folgende Wurzelgesetz an:
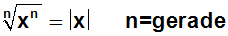
Dadurch vereinfacht sich die linke Seite der
Gleichung zu |x|. |
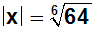 |
Jetzt rechnen die rechte Seite aus,
und
erhalten die folgende Betragsgleichung: |
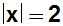 |
Diese
Betragsgleichung hat die beiden
Lösungen +2 und –2: |
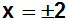 |
Weil wir innerhalb der Rechnung quadriert haben,
müssen wir die Probe machen (Quadrieren ist
nämlich keine Äquivalenzumformung, sondern
eine Folgeumformung, d.h. es können Lösungen
hinzukommen). Die Probe ergibt, dass nur –2
eine Lösung ist. |
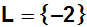 |
|
| |
|