Erscheinungsformen
einer quadratischen
Gleichung |
 |
Faktorisierte Form: (x+a)·(x+b) = 0 |
|
Manchmal kann man eine quadratische
Gleichung nicht auf Anhieb
erkennen. Ein Beispiel ist die sogenannte faktorisierte Form einer
quadratischen Gleichung (auch Produktform genannt):
(x+a)·(x+b)=0
Das die Gleichung (x+a)·(x+b)=0 eine quadratische Gleichung ist,
erkennt man, wenn man die Klammern ausmultipliziert:
(x+a)·(x+b)=0 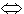 x²+ax+bx+ab=0 x²+ax+bx+ab=0 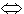 x²+(a+b)x+ab=0 x²+(a+b)x+ab=0
Ein Sonderfall liegt übrigens vor, wenn a=b:
(x+a)·(x+a)=0 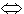 (x+a)²=0 (x+a)²=0
Die linke Seite der letzten Gleichung ist dann ein Binom.
|
 |
Die Form: (x+a)·(x+b) = c |
|
Eine zur Faktorisierten Form
ähnliche Form ist die Form:
(x+a)·(x+b)=c
Auch diese Form kann man durch Ausmuliplizieren der
Klammern in die Allgemeine Form einer quadratischen
Gleichung bringen.
Und auch hier gibt es wieder den Sonderfall a=b:
(x+a)·(x+a)=c 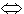 (x+a)²=c (x+a)²=c
Dieser Sonderfall wird noch eine wichtige Rolle bei
der Entwicklung eines "Lösungsverfahrens für
quadratische Gleichungen" spielen. |
|