 |
Was ist ein
reinquadratische Gleichung? |
|
Eine
reinquadratische
Gleichung ist eine Quadratische Gleichung,
bei der die Variable x nur quadratisch vorkommt, aber nicht linear:
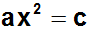
Nun ein Gegenbeispiel: Die folgende Quadratische Gleichung ist
nicht reinquadratisch, weil x auch linear vorkommt (also ohne
Exponent):
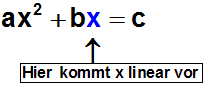
|
 |
1.Sonderfall:
Absolutglied c gleich Null |
|
In diesem Fall
wird
die reinquadratische Gleichung ax2=c
also zur Gleichung ax2=0.
Dieser Sonderfall hat nur eine Lösung: x=0
Dies folgt aus dem "Satz vom Nullprodukt":
Ein Produkt (hier: x2) ist genau dann gleich Null,
wenn mindestens ein Faktor gleich Null ist.
|
 |
2. Sonderfall:
Absolutglied c negativ |
|
Ist a eine
nicht-negative Zahl und c negativ, dann
hat die Gleichung ax²=c
keine
Lösung im Bereich
der reellen Zahlen, denn das Quadrat einer Zahl
(hier: x) ist nie negativ, und somit kann die linke Seite nie negativ
werden,
und somit kann die linke Seite nie gleich der rechten Seite werden.
Beispiel:

|
 |
3. Sonderfall: a
und c negativ |
|
Sind in der
Gleichung ax²=c die Formvariablen a und c beide negativ,
dann braucht man die Gleichung nur mit –1 multiplizieren, und es liegt
kein Sonderfall mehr vor. Beispiel:
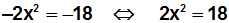
|
|
(c) www.mathematik.net - Josef Raddy
|