| Die Wurzel
aus x² |
 |
Ein häufig gemachter Fehler |
|
Wir wollen auf dieser Seite auf einen Fehler
hinweisen, der beim
Lösen von Gleichungen des Typs x²=c häufig gemacht wird.
Wir betrachten also die Gleichung:

Nun ziehen wir auf beiden Seiten der Gleichung die Wurzel. Dies stellt
noch keinen Fehler dar, denn Wurzelziehen ist eine Äquivalenzumformung
(d.h. die Lösungsmenge der Gleichung verändert sich nicht):

Nun könnte man meinen, daß sich hier Quadrieren und Wurzelziehen
gegenseitig aufheben, wie wir im Kurs "Wurzelrechnung" gelernt haben
Es würde das falsche (weil unvollständige) Ergebnis erhalten:

Wir sehen, daß das Ergebnis unvollständig und daher falsch ist,
denn die (richtige) Lösung lautet:

Um den Fehler zu finden, betrachten wir nochmal die 2.Gleichung:

Der Fehler ist folgender: Auf der linken Seite der Gleichung wurde
fälschlicherweise angenommen, dass sich Wurzelziehen und Potenzieren
gegenseitig aufheben, d.h. das folgende Gesetz wurde angewendet:
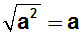
Die Regel, dass sich Potenzieren und Radizieren aufheben, gilt jedoch
nur für nicht-negative Radikanden, d.h. das Gesetz lautet
richtig:
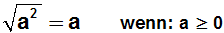
Ob unsere Basis nicht-negativ ist, wissen wir jedoch nicht,
weil x eine Unbekannte ist, die ja erst berechnet werden soll!
Daher muß ein ähnliches Gesetz angewendet werden:
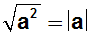
Die Lösung mit Hilfe dieses Gesetzes haben wir bereits kennengelernt.
|
|