 |
Die Binomform b(x+a)²=c
ist ein Sonderfall
einer quadratischen Gleichung |
|
Auf dieser Seite werden wir erklären,
warum dieser Sonderfall wichtig ist,
und wir werden Sonderfälle lösen.
Zuerst zeigen wir aber, dass es sich bei der Binomform
b(x+a)²=c
tatsächlich um quadratische Gleichungen handelt.
Dazu müssen wir nur die Klammer ausmultiplizieren:
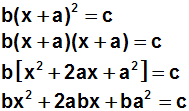
Das Produkt a·b besteht aus zwei Konstanten und kann
daher durch eine neue Konstante d ersetzt werden:
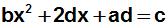
Wir bringen die Konstante c auf die linke Seite:
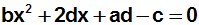
Der Term ad–c besteht nur aus Konstanten, und kann daher
ebenfalls zu einer neuen Konstanten k zusammengefaßt werden:
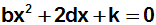
Wir sehen, dass nun die allgemeine Form einer Quadratischen Gleichung
vorliegt. Die Binomform ist also tatsächlich ein Sonderfall einer
Quadratischen Gleichung.
|
 |
Warum die Gleichung
b(x+a)²=c
wichtig ist! |
|
Die Gleichung b(x+a)²=c ist deshalb wichtig,
weil wir ihre Lösung
im nächsten Kapitel brauchen werden. Im nächsten Kapitel werden wir
nämlich ein Verfahren
entwickeln (nämlich die Quadratische Ergänzung),
mit dem wir beliebige quadratische Gleichungen lösen können.
|
 |
1.Sonderfall der Binomform: c=0 |
|
Wenn in der Binomform b(x+a)2=c das Absolutglied c
gleich Null ist,
dann wird die Gleichung zu b(x+a)2=0
und somit zu: b(x+a)(x+a)=0
.
Es liegt dann also eine "faktorisierte Form"
vor, und daher
kann man die einzige Lösung x=–a sofort ablesen. Beispiel:
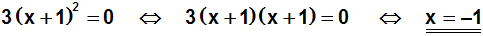
|
 |
2.Sonderfall der Binomform: b>0
und c<0 |
|
Wenn das Absolutglied c in der
Binomform b(x+a)2=c
kleiner Null ist
(und b>0),
dann hat
die Gleichung a(x+a)²=c keine (reelle) Lösung,
denn das Quadrat einer Zahl ist nie
negativ. Beispiel:
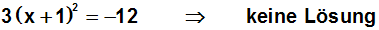
|
 |
3.Sonderfall der Binomform: b<0
und c>0 |
|
Wenn in der
Binomform b(x+a)2=c
die Zahl b negativ ist (und c positiv),
dann ist die linke Seite negativ und die rechte positiv, d.h. die
Gleichung
hat ebenfalls keine Lösung. Beispiel:
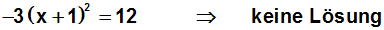
|