Lösbarkeit
und
Funktionsgraph |
 |
Lösbarkeit und Funktionsgraph |
|
Diese Seite muß überschlagen werden, wenn man
sich
noch nicht mit quadratischen Funktionen auskennt,
sondern nur mit quadratischen Gleichungen. Wir werden
das Thema nochmals im Kurs quadratische Funktionen
betrachten. |
 |
Lösbarkeit und Funktionsgraph |
|
Im einem der folgenden Kurse werden wir uns mit
den
sogenannten quadratischen Funktionen beschäftigen.
Wir werden dann sehen, daß die Nullstellen einer
quadratischen Funktion die Lösungen der zugehörigen
quadratischen Gleichung sind.
Umgekehrt sind die Lösungen einer quadratischen
Gleichungen zu finden, indem man die zugehörige
quadratische Funktion zeichnet. Die Lösungen
der quadratischen Gleichung sind die Schnittpunkte
der quadratischen Funktion mit der x-Achse (Nullstellen).
Da es nun aber quadratische Funktionen mit 0, 1 oder 2
Nullstellen gibt, gibt es auch quadratische Gleichungen mit
0, 1 oder 2 Lösungen.
|
 |
Beispiel |
|
Gegeben sei die quadratische Gleichung:
2x2
+ 6x – 20 = 0
Die zugehörige Funktion lautet:
f(x) = 2x2
+ 6x – 20
Die Funktion hat den Funktionsgraphen:
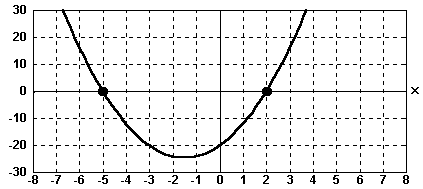
Nun können wir vom Bild ablesen: Der Graph schneidet die x-Achse
bei –5 und 2, also hat auch die zugehörige quadratische Gleichung
die Lösungen –5 und 2. |
|