Beweis des
Zerlegungssatzes |
 |
Gegeben |
|
 |
 |
Beweis |
|
In der Gleichung 1 klammern wir a aus, und
erhalten Gleichung 2::
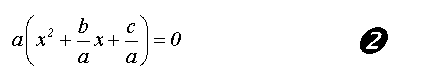
Die Nullstellen der Gleichung sind natürlich immer
noch x1 und x2.
Weil a aber laut Vorraussetzung nicht Null werden kann, müssen
die Nullstellen x1 und x2 auch die Nullstellen sein die entstehen,
wenn man die Klammer gleich Null setz. Für die Lösungen gilt
dann der Satz von Vieta:
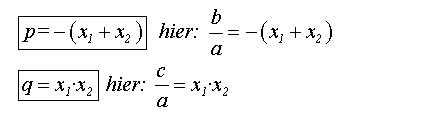
Nun können wir b/a bzw. c/a in Gleichung 2
ersetzen:
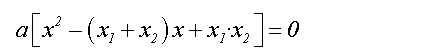
Die runde Klammer ausmultiplizieren:
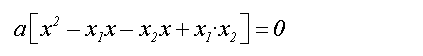
Aus den ersten beiden Summanden in der Klammer x
ausklammern,
aus den letzten beiden Summande x2 ausklammern:
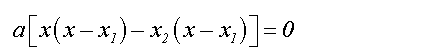
Nun die Klammer (x–x1) ausklammern:
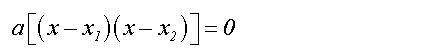
Die eckige Klammer entfällt:
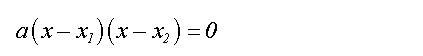
Durch Gleichsetzen dieser letzten Gleichung mit der
Gleichungen 1
erhalten wir den Zerlegungssatz:
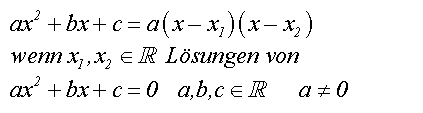 |
|