Beispiel:
Grenzwert nicht
vorhanden
|
 |
Überblick |
|
Wenn der Grenzwert nicht vorhanden ist, dann liefert das
Quotientenkriterium
keine Aussage zur Konvergenz, d.h. die Reihe kann divergieren oder
konvergieren.
Wir beweisen dies, indem wir jeweils ein Beispiel angeben.
|
 |
Fall 1: Kein Grenzwert und
divergierende Reihe |
|
Gegeben sei die folgende Reihe:
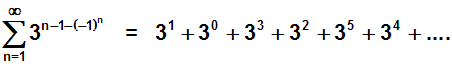
Durch umordnen erkennt man sofort, dass es sich um eine geometrische
Reihe
handelt (mit q=3), die divergiert, denn q ist größer 1:
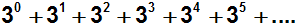
Wir wollen nun überprüfen, welches Ergebnis das Quotientenkriterium
liefert:
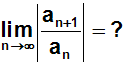
Das allgemeine Glied an können wir ablesen. Das Glied an+1
müssen wir bestimmen,
indem wir im allgemeinen Glied für n den Wert (n+1) einsetzen:
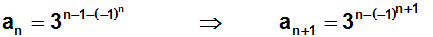
Wir setzen diese Werte in das Quotientenkriterium ein:
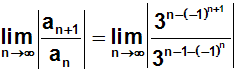
Im Exponenten des Nenners klammern wir (-1) aus:
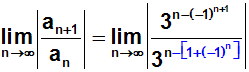
Im Zähler und Nenner wenden wir nun jeweils ein Potenzgesetz an: an–m=an/am
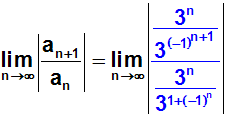
Wir lösen den Doppelbruch auf. Zur Erinnerung nochmal die Regel: Man
dividiert durch einen Bruch, indem man mit dem Kehrwert des Bruches
multipliziert:
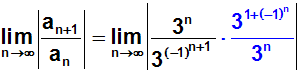
Jetzt können wir kürzen:
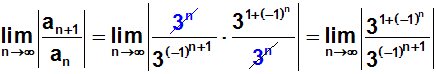
Im Exponenten des Nenners wenden wir ein Potenzgesetz an und
vereinfachen:
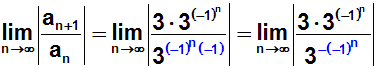
Im Nenner wenden wir nun die "Definition negativer Exponenten" an:
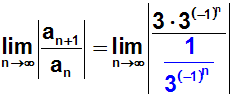
Wie bereits gerade erwähnt, dividiert man durch einen Bruch, indem man
mit dem Kehrwert multipliziert:
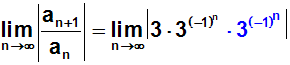
Zum vereinfachen wenden wir ein Potenzgesetz an, zum Beispiel: an·bn=(ab)n
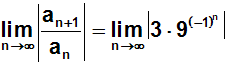
Nun sieht man: Dieser Grenzwert ist nicht definiert, denn je nachdem,
ob n gerade oder ungerade ist, schwankt der Wert zwischen 27 und 3/9.
|
 |
Fall 2: Kein Grenzwert und
konvergierende Reihe |
|
Gegeben sei die folgende Reihe:
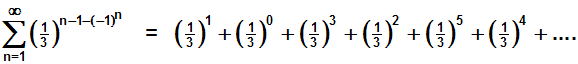
Durch umordnen erkennt man sofort, dass es sich um eine geometrische
Reihe
handelt (mit q=1/3), die konvergiert, denn q ist kleiner 1:
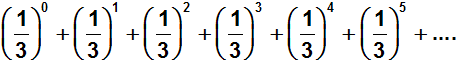
Wir wollen nun überprüfen, welches Ergebnis das Quotientenkriterium
liefert:
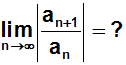
Das allgemeine Glied an können wir ablesen. Das Glied an+1
müssen wir bestimmen,
indem wir im allgemeinen Glied für n den Wert (n+1) einsetzen:
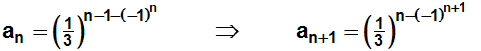
Wir setzen diese Werte in das Quotientenkriterium ein:
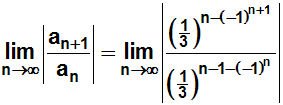
Im Exponenten des Nenners klammern wir (–1) aus:
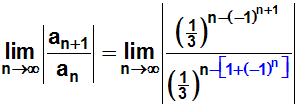
Im Zähler und Nenner wenden wir nun jeweils ein Potenzgesetz an: an–m=an/am
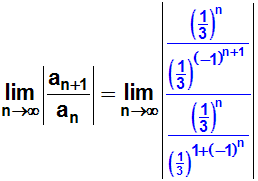
Wir lösen den Doppelbruch auf. Zur Erinnerung: Man dividiert durch
einen Bruch,
indem man mit dem Kehrwert multipliziert:
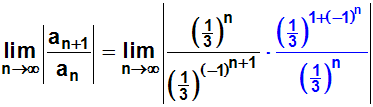
Jetzt können wir kürzen:
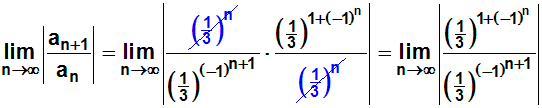
Im Exponenten des Nenners wenden wir ein Potenzgesetz an und
vereinfachen:
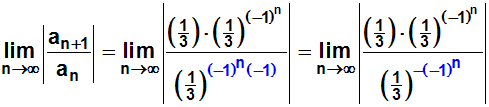
Im Nenner wenden wir nun die "Definition negativer Exponenten" an:
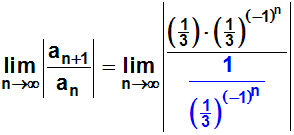
Wie bereits gerade erwähnt, dividiert man durch einen Bruch,
indem man mit dem Kehrwert dieses Bruches multipliziert:
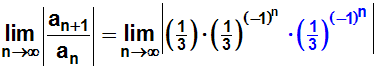
Zum vereinfachen wenden wir ein Potenzgesetz an, zum Beispiel: an·bn=(a·b)n
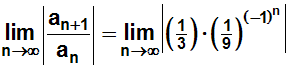
Nun sieht man: Dieser Grenzwert ist nicht definiert, denn je nachdem,
ob n gerade oder ungerade ist, schwankt der Wert zwischen
1/27 und 3.
|
| |
|