Beispiel:
Grenzwert kleiner 1 |
 |
Beispiel |
|
Beweise mit dem Quotientenkriterium, dass die folgende Reihe konvergiert:
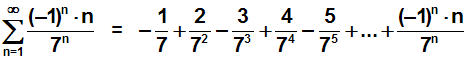
Die Formel für das Quotientenkriterium lautet:
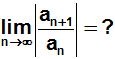
Das Formel für das n-te Glied an können wir unmittelbar aus
der Aufgabe ablesen:
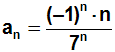
Um den Konvergenztest "Quotientenkriterium" anwenden zu können,
müssen wir aber noch an+1 bestimmen. Dies geschieht ganz
einfach dadurch,
dass wir alle "n" durch "n+1" ersetzen:
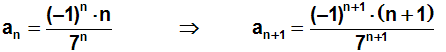
Diese beiden Werte jetzt in das Quotientenkriterium einsetzen:
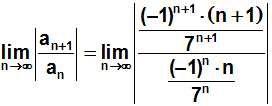
Mit den Mitteln der Bruchrechnung vereinfachen wir den Term. Zur
Erinnerung:
Man
dividiert
durch einen Bruch, indem man mit dem Kehrwert (blau) multipliziert:
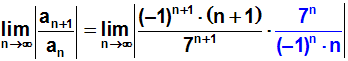
Nachdem wir die Multiplikation ausgeführt haben, erhalten wir:

Jetzt zerlegen wir 7n+1 bzw. (-1)n+1 mit Hilfe
einer Regel
aus der Potenzrechnung: am+n= am·an.
Wir erhalten:
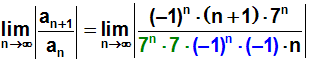
Durch das Zerlegen können wir nun kürzen:
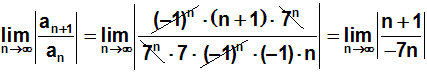
Als nächstes kürzen wir den Bruch durch die höchste Potenz von n,
d.h. wir dividieren Zähler und Nenner durch n:
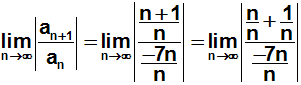
Jetzt können wir zwei der Brüche kürzen:
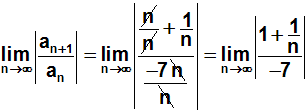
Nun führen wir den Grenzwertübergang durch, d.h. wir ersetzen
die Variable n durch Unendlich:
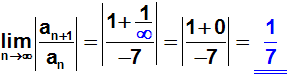
Ergebnis:
Das Quotientenkriterium liefert einen Wert (nämlich 1/7) der kleiner als
1 ist.
Daher konvergiert die gegebene Reihe, die folgendermaßen lautete:
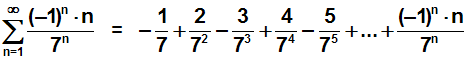
wobei wir aber nicht wissen, gegen welchen Wert die Reihe konvergiert,
denn dazu macht das Quotientenkriterium keine Angaben. |
| |
|