Beispiel:
Grenzwert gleich 1 |
 |
Beispiel |
|
Bestimme mit dem Quotientenkriterium, ob die folgende Reihe konvergiert
oder divergiert:
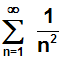
Die Formel für das Quotientenkriterium lautet:
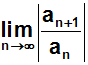
Das Formel für das n-te Glied an können wir unmittelbar aus
der Aufgabe ablesen:
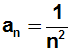
Um den Konvergenztest "Quotientenkriterium" anwenden zu können,
müssen wir aber noch an+1 bestimmen. Dies geschieht ganz
einfach dadurch,
dass wir alle "n" durch "n+1" ersetzen:
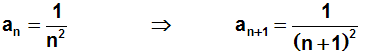
Diese beiden Werte jetzt in das Quotientenkriterium einsetzen:
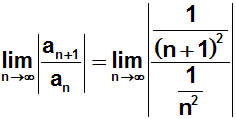
Mit den Mitteln der Bruchrechnung vereinfachen wir den Term (Zur
Erinnerung:
Man
dividiert
durch einen Bruch, indem man mit dem Kehrwert multipliziert):
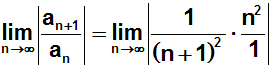
Jetzt multiplizieren wir die beiden Brüche miteinander:
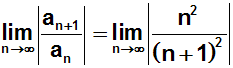
Nun multiplizieren wir die Klammer aus (am einfachsten mit der
Binomischen Formel):
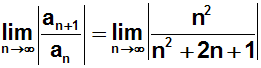
Als nächstes kürzen wir den Bruch durch die höchste Potenz von n,
d.h. wir dividieren Zähler und Nenner durch n2:
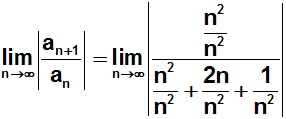
Jetzt können wir an drei Stellen kürzen:
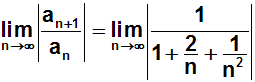
Nun führen wir den Grenzwertübergang durch, d.h. wir ersetzen n
überall durch Unendlich:
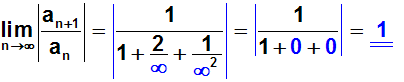
Ergebnis:
Das Quotientenkriterium versagt, denn wir erhalten den Wert 1.
Das Quotientenkriterium liefert also keine Aussage über die Konvergenz
der Reihe. |
| |
|