Beispiel:
Die Reihe der
Eulerschen Zahl |
 |
Vorbemerkungen |
|
Das folgende Beispiel stammt noch von Cauchy selbst, und erschien in
seinem Buch
"Algebraische Analysis" (1885 - Deutsche Übersetzung von Itzigsohn).
Da im Beispiel ein Majorantenkriterium benutzt wird, ist es
gegebenenfalls ratsam,
vorher den Kurs
Vergleichskriterien zu besuchen.
|
 |
Überblick über das Beispiel |
|
1. Wir wollen die Konvergenz einer bestimmten Reihe beweisen: Die Reihe
der Eulerschen Zahl
2. Laut dem Allgemeinen Konvergenzkriterium von Cauchy müssen wir dazu
beweisen,
dass der Rest Rn der Reihe beliebig klein wird,
wenn n ausreichend groß ist.
3. Dazu vergleichen wir den Rest Rn mit einer größeren Reihe,
die geometrisch ist,
und deren Grenzwert sich leicht ermitteln läßt, weil es für
den Grenzwert
von geometrischen Reihen eine Formel gibt.
Kurz gesagt: Im Schritt 3 wenden wir das
Majorantenkriterium an.
|
 |
Beispiel: Die Reihe der Eulerschen Zahl |
|
Gegeben sei folgende Reihe:
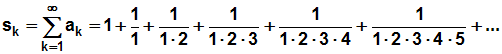
Die Terme im Nenner nennt man übrigens
Fakultäten, aber
das spielt hier keine Rolle.
Nun betrachten wir den Rest Rn dieser Reihe:
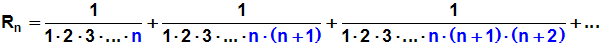
Nach dem Allgemeinen Konvergenzkriterium von Cauchy konvergiert
eine
Reihe genau dann, wenn man den Rest Rn beliebig klein machen kann.
Um zu zeigen, dass der Rest beliebig klein wird, wenden wir ein
Vergleichskriterien an,
und vergleichen den Rest Rn (der selbst eine Reihe ist) mit
folgender geometrischen Reihe,
bei welcher der Quotient zweier aufeinanderfolgender Glieder 1/n
lautet:
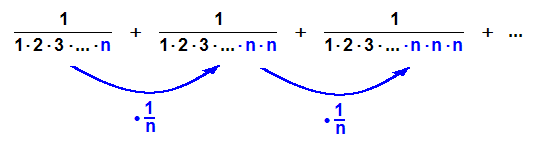
Die Glieder dieser geometrischen Reihe sind größer als die Glieder der Reihe Rn,
denn die Nenner
der Brüche sind jeweils kleiner. Wenn nun diese geometrische Reihe
beliebig klein wird (wenn n groß wird), dann wird die Reihe Rn
(der Rest) erst recht beliebig klein.
Fazit:
Wir müssen also beweisen, dass diese geometrische Reihe beliebig klein
wird.
Zunächst schreiben wir die geometrische Reihe aber etwas
übersichtlicher (Bruchrechnung):
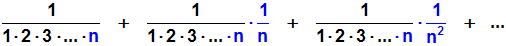
Weil der Quotient q=1/n kleiner 1 ist (wenn man n>1 wählt) konvergiert
diese Reihe,
und wir können ihren Grenzwert mit der üblichen Formel für geometische
Reihen berechnen:

Nach den Regeln der Bruchrechnung (Multiplikation von Brüchen) dürfen
wir nun schreiben:
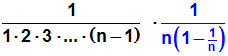
Im zweiten Bruch kann man die Klammer ausmultiplizieren::
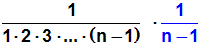
Man erkennt nun: Dieses Produkt (welches der geometrischen Reihe
entspricht)
wird beliebig klein, wenn man n ausreichend groß wählt.
Aufgrund des Vergleichskriteriums wird somit auch der Rest Rn
(d.h. die Reihe Rn) beliebig klein.
Und weil der Rest Rn beliebig klein wird, konvergiert
auch die gegebene Reihe aufgrund
des Allgemeinen Konvergenzkriteriums von Cauchy, was zu beweisen
war.
Nebenbei bemerkt: Der Wert, gegen den diese Reihe konvergiert,
ist die berühmte Eulersche Zahl e, wobei e
≈ 2,7182818 |
| |
|