| ZURÜCK | |
| Info-Seite | Vorkenntnisse: ... Themen: ... Infos: www.mathematik.net |
| Definition des Skalarproduktes |
Das
Skalarprodukt ist definiert als das Produkt aus dem Betrag von und dem Betrag der Projektion von |
| Formel für das Skalarprodukt |
Als Formel
lautet das Skalarprodukt: |
| Beispiel dazu | Einfaches Beispiel |
| Physikalische Bespiel |
In der
Physik tritt das Skalarprodukt u.a. bei der Berechnung der mechanischen Arbeit auf. |
| Skalarprodukt orthogonaler Vektoren |
Das
Skalarprodukt |
| Gesetze des Skalarproduktes |
Das
Skalarprodukt ist kommutativ: Das Skalarprodukt ist distributiv: k·( 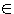 R RDas Skalarprodukt ist im allgemeinen nicht assoziativ: ( 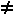 Das Skalarprodukt ist aber gemischt assoziativ: (k· 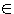 R R |
| Quadrat eines Vektors |
Das
Quadrat eines Vektors ist gleich dem Quadrat seines Betrages: |
| Skalarprodukt in Koordinaten- darstellung |
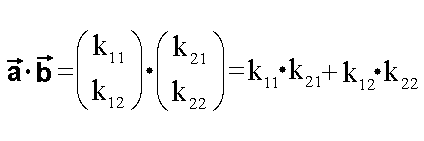 |
| Beispiel dazu | Ein Beispiel zum Skalarprodukt in Koordinatendarstellung |
| Beweis der Formel |
Beweis der Formel |