Definition
des Skalar-
produktes |
 Definition des Skalarprodukt
Das Skalarprodukt  · zweier
Vektoren und
ist definiert als das Produkt aus dem Betrag von
und dem Betrag der Projektion von auf :
· = || · |Projektion von auf |
|
Beispiel
Gegeben sind die Vektoren und , gesucht sei ihr
Skalarprodukt ·:
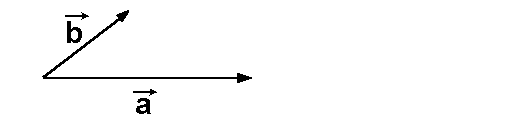Zunächst bilden wir die Projektion von auf :
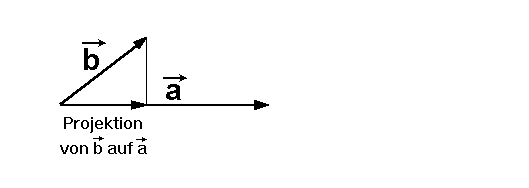Laut Definition muß man jetzt den Betrag von mit
dem Betrag der Projektion von auf multiplizieren.
Grafisch kann man das Produkt (wie jedes Produkt)
als Flächeninhalt eines Rechtecks darstellen, dessen
Seiten gleich dem Betrag von bzw. dem Betrag der
Projektion von auf sind:
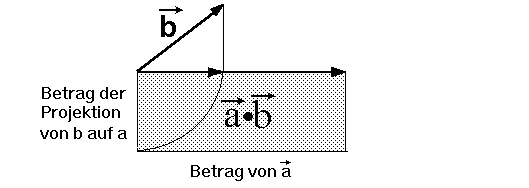Das Skalarprodukt · ist gleich der schraffierten Fläche.
|