ZURÜCK

Das Skalarprodukt 
Formel
für das
Skalarprodukt		 
a-absatz.pcx (280 Byte)Neue Formel für das Skalarprodukt
       Um nun Praktisch mit dem Skalarprodukt zu rechnen, 
       wollen wir die Formel der Vorseite in einer etwas
       anderen Form angeben:
Das Skalarprodukt ist auch definiert als:

                vekt-a.pcx (221 Byte)·vekt-b.pcx (221 Byte)   =  |vekt-a.pcx (221 Byte)| · |vekt-b.pcx (221 Byte)| · cosa-g-gama.pcx (216 Byte)  
       Wie kommt man auf diese Formel? Die alte Definition lautete:

                  vekt-a.pcx (221 Byte)·vekt-b.pcx (221 Byte)   =   |vekt-a.pcx (221 Byte)|   ·  |Projektion von vekt-b.pcx (221 Byte) auf vekt-a.pcx (221 Byte)|  

       Das zugehörige Bild sah so aus:

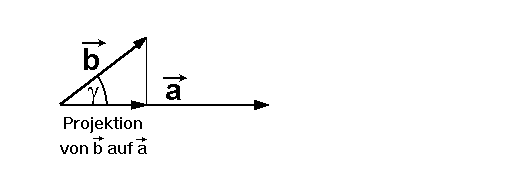       vak7s4p1.pcx (2558 Byte)
        Den Betrag der Projektion von vekt-b.pcx (221 Byte) auf vekt-a.pcx (221 Byte) kann man einfacher
        ausdrücken,  nämlich durch die Seite vekt-a.pcx (221 Byte) und den Winkel 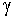a-g-gama.pcx (216 Byte):

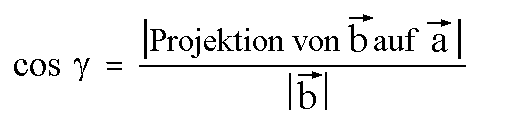     vak7s4p2.pcx (3933 Byte)

      Diese Formel stellen wir um:
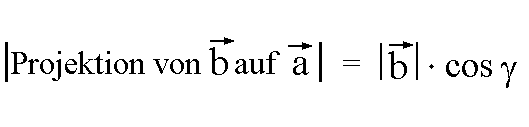      vak7s4p3.pcx (3105 Byte)
      Die Formel setzen wir nun in die alte Definition des 
      Skalarproduktes ein, und erhalten dadurch die neue Formel:

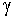
          vekt-a.pcx (221 Byte)·vekt-b.pcx (221 Byte)    =    |vekt-a.pcx (221 Byte)| · |Projektion von vekt-b.pcx (221 Byte) auf vekt-a.pcx (221 Byte)|    =    |vekt-a.pcx (221 Byte)| · |vekt-b.pcx (221 Byte)| · cosa-g-gama.pcx (216 Byte)